Seite überarbeitet Februar 2024
Kontakt
Programmübersicht
Bestelltext
Infos auf dieser Seite ... als pdf 
Eingabeoberfläche .................
Ergebnisübersicht ..................
Elast. Spannungsnachweis ....
Berechnungseinstellungen .....
Konturenplot ..........................
Plast. Spannungsnachweis ....
Schnittgrößen .......................
Querschnittsnachweise ..........
Nachweise Aluminium ............
Schnittgrößenimport ..............
Theorie .................................
Beschreibung Ergebnisse .......
Bild vergrößern
Querschnittsnachweise EC 3 und EC 9
Das Programm 4H-EC3QN führt die Spannungsnachweise für beliebige Querschnitte unter zweiachsiger Belastung nach Eurocode 3 (Stahl) bzw. Eurocode 9 (Aluminium).
Die zugehörigen Eingabeparameter werden in eigenen Registerblättern verwaltet, die über folgende Symbole
die dahinter liegende Parameterauswahl kenntlich machen.
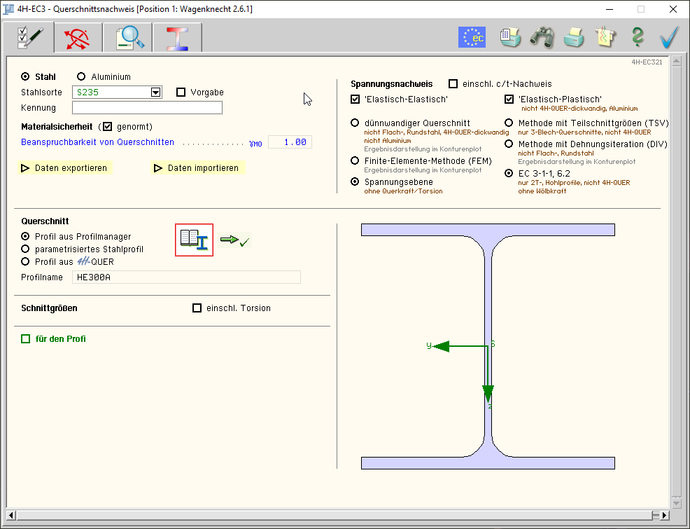
Rechenlaufsteuerung / Material / Geometrie
Im ersten Registerblatt werden die wesentlichen Parameter zum Ablauf der Berechnung festgelegt.
Dazu gehören die Materialangaben, die Materialsicherheitsbeiwerte, die Querschnittsgeometrie.
Weiterhin können die zu führenden Nachweise ausgewählt werden.
Der Querschnitt wird zur Info maßstäblich am Bildschirm dargestellt.
Bemessungsschnittgrößen
Die Schnittgrößen werden im zweiten Registerblatt festgelegt und können entweder 'per Hand'
eingegeben oder aus einem 4H-Stabwerksprogramm importiert werden.
Tabellarische Ergebnisübersicht
Im dritten Registerblatt werden die Ergebnisse (Ausnutzungen) lastfallweise und detailliert im Überblick dargestellt.
Konturendarstellung von Ergebnissen
Im vierten Registerblatt werden ausgewählte Ergebnisse als Konturenplot dargestellt.
nationaler Anhang
Weiterhin ist zur vollständigen Beschreibung der Berechnungsparameter der dem Eurocode zuzuordnende nationale Anhang zu wählen.
Über den NA-Button wird das entsprechende Eigenschaftsblatt aufgerufen.
Ausdrucksteuerung
Im Eigenschaftsblatt, das nach Betätigen des Druckeinstellungs-Buttons erscheint, wird der Ausgabeumfang der Druckliste festgelegt.
Druckliste einsehen
Das Statikdokument kann durch Betätigen des Visualisierungs-Buttons am Bildschirm
eingesehen werden.
Ausdruck
Über den Drucker-Button wird in das Druckmenü gewechselt, um das Dokument auszudrucken.
Hier werden auch die Einstellungen für die Visualisierung vorgenommen.
Planbearbeitung
Über den Pläne-Button wird das pcae-Programm zur Planbearbeitung aufgerufen.
Der aktuelle Querschnitt wird im pcae-Planerstellungsmodul dargestellt, kann dort
weiterbearbeitet, geplottet oder im DXF-Format exportiert werden.
Onlinehilfe
Über den Hilfe-Button wird die kontextsensitive Hilfe zu den einzelnen Registerblättern aufgerufen.
Eingabe beenden
Das Programm kann mit oder ohne Datensicherung verlassen werden.
Bei Speichern der Daten wird die Druckliste aktualisiert und in das globale Druckdokument eingefügt.
im Register 1 (s. Eingabeoberfläche) werden die allgemeinen Einstellungen der Berechnung festgelegt.
Material
Der Querschnitt kann aus Stahl oder Aluminium bestehen.
Da die Beschreibung der Stahlparameter für eine Berechnung nach EC 3 programmübergreifend identisch ist,
wird auf die allgemeine Beschreibung der Stahlsorten verwiesen.
Aluminium
Aktuell werden folgende Aluminiumlegierungen (typisiert in EC 9-1-1, 3.2.2) vorgehalten
Knetlegierungen für Bleche, Bänder und Platten (s. Tab. 3.2a)
EN-AW 3004
EN-AW 3005
EN-AW 3103
EN-AW 5005 / 5005A
EN-AW 5052
EN-AW 5049
EN-AW 5454
EN-AW 5754
EN-AW 5083
EN-AW 6061
EN-AW 6082
EN-AW 7020
EN-AW 8011A
Knetlegierungen für Strangpressprofile, stranggepresste Rohre, Stangen und gezogene Rohre (s. Tab. 3.2b)
EN-AW 5083
EN-AW 5454
EN-AW 5754
EN-AW 6060
EN-AW 6061
EN-AW 6063
EN-AW 6005A
EN-AW 6082
EN-AW 7020
Knetlegierungen für Schmiedeerzeugnisse (s. Tab. 3.2c)
EN-AW 5754
EN-AW 5083
EN-AW 6082
Natürlich können die zur Bemessung in diesem Programm verwendeten Parameter verändert und an geeignete Produktnormen angepasst werden.
 
Die 'Legierung' steht somit als Synonym für die charakteristischen Werte der 0.2%-Dehngrenze fo und der Zugfestigkeit fu sowie den Elastizitätsmodul E, die für die Berechnung verwendet werden.
Zur genaueren Bezeichnung der Legierung steht ein Text-Eingabefeld zur Verfügung.
Materialsicherheitsbeiwerte
Für den Spannungsnachweis n. EC 3-1-1 wird folgender Materialsicherheitsbeiwert verwendet
Aluminium hat n. EC 9-1-1 folgenden Sicherheitsbeiwert
Die Werte können entweder den entsprechenden Normen (s. Nationaler Anhang) entnommen oder
vom Anwender vorgegeben werden.
Allgemeines
Im Programm 4H-EC3QN besteht die Möglichkeit, die Eingabedaten über die Copy-Paste-Funktion von einem
Bauteil in ein anderes desselben Typs zu exportieren.
Dazu ist der aktuelle Datenzustand im abgebenden Bauteil über den Button Daten exportieren in die
Zwischenablage zu kopieren und anschließend über den Button Daten importieren aus der Zwischenablage
in das aktuell geöffnete andere Bauteil zu übernehmen.
Querschnitt
Der Querschnitt kann entweder über den pcae-eigenen Profilmanager in das Programm importiert oder als
parametrisiertes Stahlprofil eingegeben werden.
Ist das pcae-Programm 4H-QUER, Querschnittswerte, installiert, kann alternativ ein beliebiger Querschnitt
erstellt und in das Programm 4H-EC3QN geladen werden.
Um ein Profil aus dem Angebot des Profilmanagers zu wählen, ist der grün unterlegte Pfeil zu betätigen.
Das externe Programm wird aufgerufen und ein Profil kann
aktiviert werden. Bei Verlassen des Profilmanagers werden die benötigten Daten übernommen und der Profilname protokolliert.
Die hinterlegten Profilparameter können am Bildschirm
eingesehen werden, wenn auf parametrisiertes Stahlprofil umgeschaltet wird.

Zur Definition eines parametrisierten Stahlprofils ist zunächst
die Profilklasse festzulegen.

In Abhängigkeit davon werden Profilhöhe, Stegdicke sowie ggf. Flanschbreiten und -dicken zur Eingabe angeboten.
Flanschneigungen werden nicht berücksichtigt.
Bei gewalzten Doppel-T-Profilen wird der Ausrundungsradius r zwischen Flansch und Steg bzw. r2 an den äußeren Flansch-rändern geometrisch berücksichtigt, während geschweißte Blechprofile mit Schweißnähten (Kehlnähte der Dicke a oder durchgeschweißte Stumpfnähte) zusammengefügt sind.
Diese Schweißnähte werden nicht nachgewiesen.
Ist das pcae-Programm 4H-QUER installiert, wird eine entsprechende Eingabemöglichkeit angeboten.
Zunächst ist festzulegen, ob der Querschnitt dünnwandig
(über die Mittellinien) oder dickwandig (polygonal) beschrieben werden soll.
Das externe Programm wird über den gelb unterlegten Aktions-Button mit dieser Vorgabe aufgerufen.
In einer grafischen Oberfläche kann dort der Querschnitt konstruiert oder aus einer Bibliothek geladen und an das aufrufende Programm 4H-EC3QN übergeben werden.
Der 4H-QUER-Querschnitt muss den Vorgaben (dünnwandig oder dickwandig) entsprechen.
Weitere Informationen zur Bedienung des Programms 4H-QUER s. zugehöriges Handbuch.
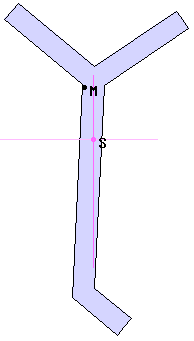
Zur visuellen Kontrolle der Eingabeparameter wird der Querschnitt maßstabsgetreu am Bildschirm dargestellt.
Schwerpunkt S, Schubmittelpunkt M und die Hauptachsen sind markiert.
Spannungsnachweis
Das Programm 4H-EC3QN bietet drei elastische und drei plastische Spannungsnachweise an.
Die nachweisbezogenen Einschränkungen bzgl. Material, Querschnittstyp oder Schnittgrößen sind
am Bildschirm angegeben.
Optional können ein elastischer und ein plastischer Nachweis in einem Rechengang geführt werden.
Die Beschreibung der Nachweise erfolgt hier.
Bedingung für die Gültigkeit der Verfahren ist, dass der Querschnitt nicht beulgefährdet ist. Ein vereinfachter Beulnachweis wird über das c/t-Verhältnis erbracht. Ein entsprechender Nachweis kann deaktiviert werden.
Der Querschnitt kann elastisch oder plastisch nachgewiesen werden, wobei die Schnittgrößen elastisch
berechnet werden.
Die Anwendungsvoraussetzungen für die einzelnen Verfahren sind am Bildschirm in Kurzform und in der folgenden Tabelle ausführlich dargestellt.
Zur Info ist zusätzlich angegeben, bei welchen Querschnittstypen Verwölbung auftreten kann.
Mit einem Sternchen sind diejenigen Nachweise gekennzeichnet, deren Ergebnisse als Konturenplot darstellbar sind.
Konturenplot
Die Ergebnisse der gekennzeichneten Nachweise können je Lastkombination als Konturenplot und/oder tabellarisch ausgegeben werden.
Für jeden Ergebnissatz wird zusätzlich zu den resultierenden Nachweisergebnissen ein eigener Konturenplot ausgegeben, wohingegen die Tabelle um die gewählten Ergebnisspalten erweitert wird.
In den Tabellen können entweder sämtliche Knotenergebnisse (nicht empfehlenswert) oder die je Ergebnisspalte maßgebenden Ergebnissätze (s. Ausdrucksteuerung, optimierte Tabelle) zeilenweise dargestellt werden. Die Extremalwerte sind markiert.
Wird einzig eine elastische Berechnung mit der Finite-Elemente-Methode durchgeführt, kann in der schlussendlichen Zusammenfassung die flächenverteilte Ausnutzung des Querschnitts als Resultierende aller Lastkombinationen grafisch und tabellarisch ausgegeben werden.
Bei besonders komplexen Querschnittsformen ist es übersichtlicher, den Konturenplot in Großformat auszugeben.
Außerdem kann die Farbpalette analog der Visualisierung gewählt werden.

Der Übersichtlichkeit halber kann an dieser Stelle die Verwendung von Torsion oder Verwölbung ausgeschaltet werden.
Im Register Schnittgrößen wird die Einstellung berücksichtigt, indem die entsprechenden Tabellenspalten
deaktiviert werden.

Versierte Programmanwender (Profis) können die verwendeten Verfahren beeinflussen.

Die Bedeutungen der Einstellungen werden bei Beschreibung der Nachweisverfahren erläutert.
pcae empfiehlt, die folgenden Parameter nicht zu ändern
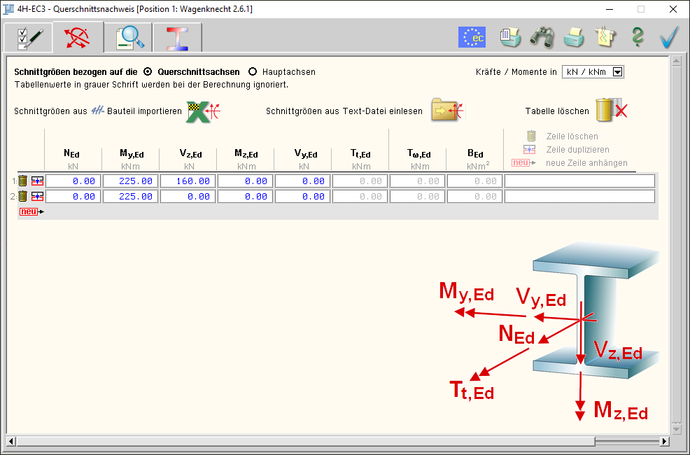
das zweite Register beinhaltet die Masken zur Eingabe der Bemessungsschnittgrößen
Bild vergrößern
Die Schnittgrößen werden als Bemessungsgrößen mit der Vorzeichendefinition
der Statik eingegeben, wobei das x,y,z-Koordinatensystem dem l,m,n-System
der pcae-Tragwerksprogramme entspricht.
Es können bis zu 10.000 Schnittgrößenkombinationen eingegeben werden.
Bei Übernahme der Schnittgrößen aus einem Tragwerksprogramm ist
zu beachten, dass sie sich auch bei unsymmetrischen Querschnitts-profilen (z.B. L-Profil) auf das Stab-Koordinatensystem und nicht auf
das Hauptachsensystem (pcae-Bezeichnung: ξ,η,ζ) beziehen!
Die Schnittgrößen können wahlweise in folgenden Einheiten vorliegen
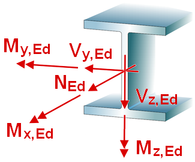
Im Standardfall
bewirken die Schnittgrößenkombinationen N, My, Vz eine Biegung um die starke Achse des Querschnitts
bewirken die Schnittgrößenkombinationen N, Mz, Vy eine Biegung um die schwache Achse des Querschnitts
ist das Torsionsmoment Tt (St.Venant'sche bzw. primäre Torsion) nur für Hohl- und Vollquerschnitte relevant
wirken die Verwölbungsgrößen Tω, B (sekundäre Torsion, Bimoment) nur bei Querschnitten mit abstehenden Querschnittsteilen
Sind Torsions- oder Verwölbungsschnittgrößen für den betrachteten Querschnitt nicht maßgebend und sollen nicht untersucht werden, können die entsprechenden Schnittgrößenspalten deaktiviert werden, indem in Register 1 der
Profi-Button aktiviert und die entsprechende Option abgewählt wird.
Die Zahlenwerte in den Spalten sind grau dargestellt, können jedoch weiter bearbeitet werden. Bei der Bemessung werden diese Schnittgrößen ignoriert.
Da bei unsymmetrischen Querschnitten die Querschnittsachsen nicht mit der Hauptachsenrichtung übereinstimmen, besteht die Möglichkeit, die Schnittgrößen wahlweise auf die Querschnittsachsen oder Hauptachsen zu beziehen.
Die Bezeichnung der Schnittgrößen M und V wird entsprechend angepasst.
Die Berechnung des Hauptachsenwinkels ist nicht eindeutig.
pcae empfiehlt, die Schnittgrößen auf die Querschnittsachsen zu beziehen.
Schnittgrößen importieren

Detailnachweisprogramme zur Bemessung von Anschlüssen (Träger/Stütze, Trägerstöße), Fußpunkten
(Stütze/Fundament) etc. benötigen Schnittgrößenkombinationen, die häufig von einem Tragwerksprogramm zur Verfügung gestellt werden.
Dabei handelt es sich i.d.R. um eine Vielzahl von Kombinationen, die im betrachteten Bemessungsschnitt des übergeordneten Tragwerkprogramms vorliegen und in das Anschlussprogramm übernommen werden sollen.
pcae stellt neben der 'per Hand'-Eingabe zwei verschiedene Mechanismen zur Verfügung, um Schnittgrößen in das vorliegende Programm zu integrieren.
Import aus einem 4H-Programm
Voraussetzung zur Anwendung des DTE®-Import-Werkzeugs ist, dass sich ein pcae-Programm auf dem Rechner befindet, das Ergebnisdaten exportieren kann.
Eine ausführliche Beschreibung zum Schnittgrößenimport aus einem pcae-Programm befindet sich hier.
Import aus einer Text-Datei
Die Schnittgrößenkombinationen können aus einer Text-Datei im ASCII-Format eingelesen werden.
Die Datensätze müssen in der Text-Datei in einer bestimmten Form vorliegen; der entsprechende Hinweis wird bei Betätigen des Einlese-Buttons gegeben.
Anschließend wird der Dateiname einschl. Pfad der entsprechenden Datei abgefragt.
Es werden sämtliche vorhandenen Datensätze eingelesen und in die Tabelle übernommen. Bereits bestehende Tabellenzeilen bleiben erhalten.
Wenn keine Daten gelesen werden können, erfolgt eine entsprechende Meldung am Bildschirm.
das dritte Register gibt einen Überblick über die ermittelten Ergebnisse
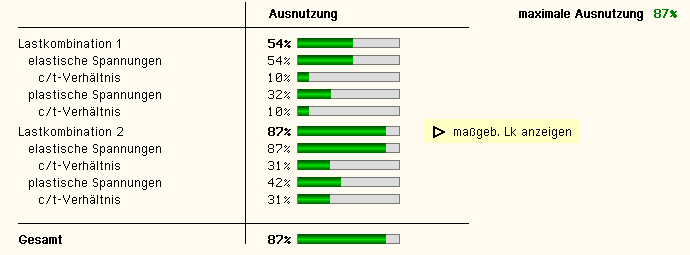
Zur sofortigen Kontrolle werden die Ergebnisse in diesem Register lastfallweise übersichtlich zusammengestellt.
Eine Box zeigt an, ob ein Lastfall die Tragfähigkeit des Anschlusses überschritten hat (rot ausgekreuzt)
oder wie viel Reserve noch vorhanden ist (grüner Balken).
Bei bis zu zehn Lastkombinationen werden zur Fehleranalyse oder zur Einschätzung der Tragkomponenten
die Einzelberechnungsergebnisse protokolliert.
Die maximale Ausnutzung wird sowohl als 'Gesamt' unterhalb der Zusammenstellung als auch am oberen
rechten Fensterrand angezeigt.
Ebenso wird die maßgebende Lastkombination gekennzeichnet und kann über den Aktionslink direkt in der
Druckliste eingesehen werden.
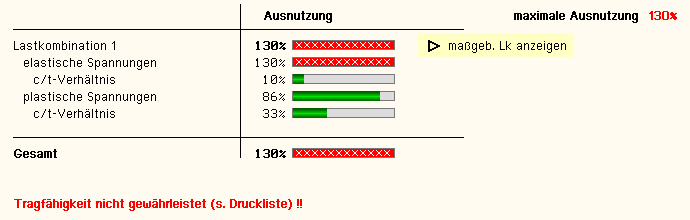
Eine Meldung zeigt an, wenn ein Fehler aufgetreten oder die Tragfähigkeit überschritten ist.
Wenn die Ursache des Fehlers nicht sofort ersichtlich ist, sollte die Druckliste in der ausführlichen Ergebnisdarstellung geprüft werden.
das vierte Register stellt für einige Nachweisverfahren die Ergebnisse grafisch dar.
Bild vergrößern
Dazu gehören die Ergebnisse der elastischen Berechnung mit dem Verfahren für dünnwandige Querschnitte und der Methode der Finiten Elemente sowie der plastischen Berechnung mit dem Verfahren der Dehnungsiteration.
Es werden die Dehnungen ε, die Spannungen σx, τ, σv und die Traglastausnutzung U visualisiert.
Liegen sowohl aus der elastischen als auch der plastischen Berechnung Ergebnisse vor, wird zunächst aus einer Listbox der Nachweistyp festgelegt.
'E-E' steht für den elastischen, 'E-P' für den plastischen Querschnittsnachweis.
Sind Ergebnisse für nur einen Nachweistyp vorhanden, wird die Listbox nicht angezeigt.
Sind elastische Nachweisergebnisse vorhanden, wird In einer weiteren Listbox der Darstellungstyp festgelegt.
Das erste Listenelement bezeichnet den Konturenplot, der für sämtliche Ergebnisse zur Verfügung steht und über eine abgestufte Palette den Werteverlauf darstellt.
Für ein besseres Verständnis der räumlichen Verformung kann das zweite Listenelement, die Deformationsgrafik, zur Darstellung der Dehnungen angewählt werden.
Ergebnisse der plastischen Berechnung können nur als Konturenplot angezeigt werden.
Aus einer weiteren Listbox wird nun eine Lastkombination ausgewählt.
Zusätzlich zu den Lastkombinationen können die Ergebnisse, die zur maximalen Ausnutzung gehören, dargestellt werden.
Es stehen die Ergebnisse der
der Dehnung ε,
Spannungen σx, τ, σv und
Spannungsausnutzung U
zur Verfügung.
Die Zahlenwerte der Ergebnisse werden angezeigt, wenn der Maus-Cursor über die Grafik bewegt wird.
Aus zwei Farbpaletten kann die Einfärbung des Konturenplots für Dehnungen und Normalspannungen gewählt werden.
Die Bandbreite der Palette wird in der Legende angezeigt und
bildet jeweils den Extremwert positiv und negativ ab.
Können die Ergebniswerte nicht negativ werden (Schubspannung, Vergleichsspannung, Ausnutzung), wird eine neutrale Palette verwendet.
Auch hier wird die Bandbreite angezeigt.
Sonderfall: Die Ausnutzung hat eine feste Bandbreite von 0 bis 1. Überschreitet die vorhandene Ausnutzung den maximal zulässigen Bereich, werden die Querschnittsflächen rot eingefärbt.
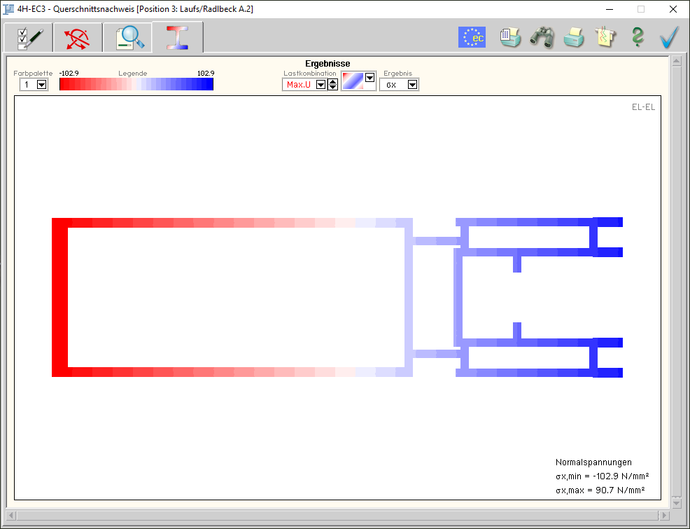
Darstellung der Ergebnisse am Bildschirm (Beispiel: U 100 mit Wölbbimoment BEd = 0.15 kNm2)
Konturenplot der Ausnutzungen mit Angabe eines beliebig ausgewählten Berechnungswerts.
Die maximale Ausnutzung ist protokolliert. Bereiche, in denen U ≥ 1, sind rot unterlegt.
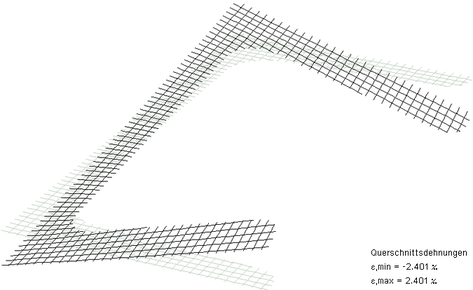
Deformationsgrafik der Querschnittsdehnungen. Die Extremalwerte sind angegeben.
Zur Orientierung ist das unverformte System in grau eingefügt.
Zur Darstellung des Druckdokuments s. Beschreibung der Ergebnisse.
Es werden sechs Spannungsnachweise, davon drei für den elastisch-elastischen und drei für den
elastisch-plastischen Nachweis angeboten.
Die Schnittgrößenermittlung erfolgt auf Grundlage der Elastizitätstheorie, der Nachweis kann elastisch und plastisch geführt werden.
elastischer Spannungsnachweis
als dünnwandiger Querschnitt
Finite-Elemente-Methode
Spannungsebene
plastischer Spannungsnachweis
Methode mit Teilschnittgrößen
Methode mit Dehnungsiteration
EC 3-1-1, 6.2
Zusätzlich kann für dünnwandige Querschnitte der vereinfachte Beulnachweis (c/t-Nachweis) in die Berechnung der Tragfähigkeit einbezogen werden.
Die Nachweise sind teilweise eingeschränkt, d.h. für einige Querschnittstypen oder bestimmte Schnittgrößenarten
nicht nutzbar.
Bei einigen Nachweisen kann eine Analyse der Spannungen und Dehnungen über Querschnittsgrafiken am
Bildschirm durchgeführt werden.
Die auf den Querschnitt einwirkenden Schnittgrößen erzeugen Spannungen, die materialspezifische Grenzwerte
nicht überschreiten dürfen.
Aus Normalkraft N und Biegemomenten M resultieren Normalspannungen σx, aus Querkräften V und einem Torsionsmoment Tt resultieren Schubspannungen τ.
Wirken die Querkräfte nicht im Schubmittelpunkt, wird zusätzliche Torsion erzeugt. Aufgrund des primären Torsionsmoments Tt kann eine Querschnittsverwölbung hervorgerufen werden, die zu einem sekundären Torsionsmoment Tω (zus. τ-Anteil) und einem Wölbbimoment B (zus. σx-Anteil) führt.
Der elastische Spannungsnachweis erfolgt mit dem Fließkriterium aus DIN EN 1993-1-1, 6.2.1(5)
Punktweise wird die Ausnutzung des Querschnitts berechnet mit
Die Berechnung der Normalspannungen erfolgt mit
wobei sich η, ζ auf das Hauptachsensystem beziehen (s. Theorie).
Die Unterschiede in den Verfahren zum elastischen Querschnittsnachweis liegen in der Berechnung der Schubspannungen aus Querkraft und Torsion.
Der plastische Spannungsnachweis wird ganzheitlich am Querschnitt betrachtet und für Normal- und Schubspannungen gemeinsam durchgeführt. Die Querschnittsausnutzung wird über Laststeigerung ermittelt
(nicht bei EC 3-1-1, 6.2).
Der plastische Nachweis erfolgt nur für Stahlquerschnitte.
Nach EC 3-1-1, 5.5, ist über die Klassifizierung der Querschnitte die Begrenzung der Beanspruchbarkeit und Rotationskapazität durch lokales Beulen festzustellen.
Querschnitte der Klassen 1 und 2 dürfen plastisch und elastisch nachgewiesen werden, für Querschnitte in
Klasse 3 kann nur der elastische Nachweis geführt werden. Querschnitte in höheren Querschnittsklassen sind beulgefährdet und müssen gesondert untersucht werden.
Die Querschnittsklassifizierung erfolgt nach dem c/t-Verhältnis der druckbeanspruchten Querschnittsteile,
wobei c der Länge des Querschnittsteils und t dessen Dicke entspricht.
Die Ausnutzung berechnet sich mit
Im Folgenden werden die theoretischen Grundlagen zur Berechnung der Querschnittswerte dargelegt.
Beachte: Das hier eingeführte l,m,n-Koordinatensystem entspricht dem x,y,z-Koordinatensystem
der Querschnittsnachweise.
Koordinatensysteme
Die klassische Stabtheorie geht von der Formerhaltung des Querschnitts aus. Die Querschnittslage lässt sich
im lokalen xyz-Querschnittskoordinatensystem über drei Verschiebungen ux, uy, uz und drei Verdrehungen
φx, φy, φz beschreiben.

In der Theorie der Wölbkrafttorsion wird die Verwölbung des Querschnitts durch das Produkt der Einheitsverwölbung ω
mit der Verwindung ψx beschrieben.
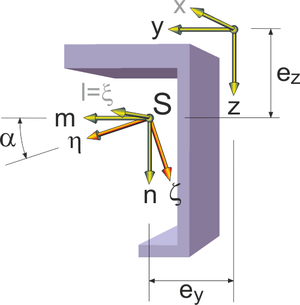
Neben dem xyz-Querschnittskoordinatensystem, in dem der Querschnitt modelliert wird, gibt es weiterhin das durch den Schwerpunkt S mit den Koordinaten (ey, ez) verlaufende lmn-System, dessen Achsen parallel zu den xyz-Achsen verlaufen (Entkopplung der Fläche und der Trägheitsmomente), sowie
das durch S verlaufende ξηζ-Hauptachsensystem (Entkopplung der Trägheitsmomente).
Zur Beschreibung der Torsion wird der Schubmittelpunkt M
mit den Koordinaten (yM, zM) als Drehpunkt verwendet (z.B. normierte Einheitsverwölbung ω, Entkopplung der Biegung und Wölbkrafttorsion).
Die Berechnung der Querschnittswerte und der Spannungen
aus Biegung erfolgt am vollständigen Modell mit Verschneidungen, Abschrägungen und Ausrundungen.
Die Verteilung der Schubflüsse, der Schubspannungen und der Verwölbung längs der Mittellinien wird am Linienmodell unter Berücksichtigung der veränderlichen Dicke ermittelt.
Schwerpunkt, Trägheitsmomente und Hauptachsen
Bei einer konstanten Spannungsverteilung verschwinden die Biegemomente im Schwerpunkt.
Die Schwerpunktskoordinaten (ey, ez) lassen sich mit der Querschnittsfläche A und den statischen Momenten Sy
bzw. Sz berechnen.


Mit den Trägheitsmomenten im Schwerpunkt lassen sich im linear elastischen Fall aus der Dehnung εS und den Krümmungen κm, κn die Schnittgrößen der Biegung ermitteln.


Das ξηζ-Hauptachsensystem ist bzgl. des Querschnittskoordinatensystems um den Winkel α verdreht.
Im Hauptachsensystem ist das Deviationsmoment Imn gleich Null, so dass die Krümmungen und Momente der Hauptbiegerichtungen entkoppelt sind.


Der Hauptachsendrehwinkel ist bis auf ein Vielfaches von 90° bestimmt. Der Winkel wird so gewählt, dass er
bzgl. des Querschnittskoordinatensystems betragsmäßig möglichst klein ist.
Verwölbung und Schubmittelpunkt
Für dünnwandige Querschnitte berechnet sich die Wölbordinate ωD,0 für den Drehpunkt D mit den Koordinaten
(yD, zD) als Integral des Hebelarms rD der Querschnittspunkte zum Drehpunkt längs der Profilkoordinate s
(β: Winkel der Tangente an die Mittellinie).


Es wird davon ausgegangen, dass die Verwölbung in Dickenrichtung konstant ist. Die mittlere Querschnittsdehnung
der zugehörigen Einheitsverwölbung ωD ist Null, so dass bei reiner Verwölbung (im linear elastischen Fall) keine Normalkraft vorhanden ist.


Die Einheitsverwölbungen mit den Drehpunkten (yD, zD) und (yM, zM) stehen in folgender Beziehung


Der Schubmittelpunkt (yM, zM) ist der Drehpunkt, für den bei reiner Verwölbung (im linear elastischen Fall) keine Biegemomente auftreten. Für den Abstand (ySM, zSM) des Schubmittelpunkts vom Schwerpunkt ergibt sich

Schnittgrößen und Spannungen
Die Schnittgrößen ergeben sich durch Integration der Normal- bzw. Schubspannungen über den Querschnitt.
Die Schnittkräfte wirken in Richtung der verformten Querschnittsachsen, die Momente drehen um die
entsprechenden Achsen in positiver Richtung (Rechte-Hand-Regel).


Mit den Biegemomenten im Hauptachsensystem, den Torsionsschnittgrößen um den Schubmittelpunkt
und den entsprechenden Trägheitsmomenten können im linear elastischen Fall die Normalspannungen
aus den Schnittgrößen ermittelt werden.


Für dünnwandige Querschnitte werden zur Berechnung des Schubflusses T und der Schubspannung τxs in
Richtung der Profilmittellinien die statischen Momente Sη, Sζ, Sω und die Profildicken t in Abhängigkeit der Profilkoordinate s benötigt.


Tt ist dabei das primäre Torsionsmoment aus St. Venant'scher Torsion und Tw das sekundäre Torsionsmoment
aus Wölbkrafttorsion.
Für Querschnitte mit geschlossenen Zellen kommen noch Schubspannungen aus den Schubflüssen der
einzelnen Zellen hinzu.
Die Faktoren θ entsprechen den Einheitsschubflüssen der entsprechenden Schnittgröße.
Die Schubspannungen aus Vη, Vζ und Tw bzw. Tt der Zellen sind nach Voraussetzung konstant in Dickenrichtung.
Die Schubspannung aus Tt der einzelnen Querschnittslinien ist in Dickenrichtung linear veränderlich und
verschwindet auf der Mittellinie.
Wagner-Effekt
Neben dem primären Torsionsmoment Tt tritt bei Berechnungen nach Theorie II. Ordnung unter Berücksichtigung
des Wagner-Effekts das Torsionsmoment Tσ infolge Normalspannungen auf.


Der Wagner-Koeffizient Kσ lässt sich aus den Schnittgrößen im Hauptachsensystem berechnen.


Die Querschnittsstrecken ergeben sich durch Integration des Quadrats des Schwerpunktabstands rS über
den Querschnitt.

Schubkorrekturfaktoren
Die Schubkorrekturfaktoren werden zur Ermittlung der Schubflächen bzw. Schubsteifigkeiten bei der Berechnung
von schubweichen Stäben benötigt.
Die mittleren Schubgleitungen γxy und γxz stehen mit den zugehörigen Querkräften in Beziehung.


ϑTy und ϑTz sind dabei die Einheitsschubflüsse der Querkräfte in y- und z-Richtung.
Aus den κ-Werten lassen sich die Schubkorrekturfaktoren in einem um den Winkel α verdrehten
Koordinatensystem berechnen.

mehrteilige Querschnitte
Falls nicht alle Querschnittsteile miteinander verbunden sind, liegt ein mehrteiliger Querschnitt vor.
Bei einem mehrteiligen Querschnitt wird davon ausgegangen, dass die einzelnen Teile durch Riegel oder Platten so miteinander gekoppelt sind, dass sie sich affin zueinander verformen.
Den Schubmittelpunkt des Gesamtquerschnitts erhält man durch gewichtete Summation der Schubmittelpunkte der Teile. Die Verwölbung mit dem Schubmittelpunkt (yM, zM) als Drehachse des i-ten Teils im Gesamtquerschnitt kann aus der Verwölbung des Teils mit dem i-ten Schubmittelpunkt (yM,i, zM,i) als Drehachse berechnet werden.
Die Verschiebung u in Richtung der Stabachse bzw. die Längsspannung für den linear-elastischen Fall kann
dann lokal für jedes Teil formuliert werden.


Die Querschnittsteile können biegesteif oder biegeschlaff miteinander verbunden sein. Die Verteilung der
Normalkräfte hängt vom Grad α der Biegekopplung ab (biegesteif: α = 1, biegeschlaff: α = 0).
Der Wert von α hat über den Steiner-Anteil der Teile Einfluss auf die Trägheitsmomente des Gesamtquerschnitts.
Die Querschnittswerte des Gesamtquerschnitts erhält man durch Summation der Querschnittswerte der Teile.


Die Normalkräfte verteilen sich im Verhältnis der Teilflächen.


Wenn die Krümmungen der Querschnittsteile identisch sind, lassen sich die (linear elastischen) Momente Mm,i
und Mn,i der Teile bzgl. ihrer Schwerpunkte aus den Momenten Mm und Mn des Gesamtquerschnitts berechnen.


Für die Aufteilung der Querkräfte ergeben sich dann ähnliche Beziehungen.


Die Torsionsmomente und das Wölbbimoment verteilen sich im Verhältnis der Querschnittswerte auf
die einzelnen Teile.


Die Schnittgrößen des Gesamtquerschnitts erhält man durch Summation der Teilschnittgrößen.

plastische Widerstandsmomente
Die plastischen Grenzmomente können mit Hilfe der plastischen Widerstandsmomente berechnet werden.
Die zugehörige Spannungsverteilung erzeugt dabei keine Normalkraft; die resultierenden Momente beziehen
sich auf den Schwerpunkt.
Für jede Achse, um die das Grenzmoment wirkt (z.B. m-, n-, η-, ζ-Achse), sind zwei evtl. unterschiedliche Widerstandsmomente von Interesse.

Das maximale plastische Widerstandsmoment liefert das maximal mögliche Moment um die betrachtete Achse.
Die neutrale Achse ist parallel zur Achse und teilt die Querschnittsfläche in zwei gleiche Teile. Das zum
Grenzmoment senkrecht wirkende Moment kann dabei von Null verschieden sein (z.B. unsymmetrische
Querschnitte, gedrehte Hauptachsen).

Die Spannungsverteilung des reduzierten plastischen Widerstandsmoments liefert das maximal mögliche Moment
um die betrachtete Achse unter der Zusatzbedingung, dass das zum Grenzmoment senkrecht wirkende Moment
gleich Null ist. Die neutrale Achse ist evtl. zur Momentenachse verdreht.

Die Berechnung der Widerstandsmomente erfolgt mit Hilfe der Dehnungsiteration. Als Stoffgesetz wird hierbei
eine bilineare Spannungs-Dehnungs-Beziehung verwendet. Zu dem betrachteten Moment wird iterativ ein Dehnungszustand unter Berücksichtigung der Grenzdehnung (z.B. 20%) und der zu beachtenden Neben-
bedingungen (keine Normalkraft, evtl. kein Quermoment) ermittelt. Aus der zugehörigen Spannungsverteilung
lassen sich das Grenzmoment und das Widerstandsmoment berechnen.
Berechnung von Wölbfunktion und Torsionskennwerten mit der Methode der Finiten Elemente
Die Verwölbung der primären und sekundären Torsion bzw. des Querkraftschubs berechnen sich mit der Methode
der Finiten Elemente aus der Potentialgleichung (in den Hauptachsenkoordinaten η,ζ)


Längs der Querschnittsränder gilt die Randbedingung (mit dem Normalenvektor (nη, nζ))


Es werden folgende Funktionen f(η,ζ) und g(η,ζ) für die einzelnen Problemstellungen angesetzt


Dabei ist ωM die normierte Verwölbung der primären Torsion und (ηM, ζM) der Schubmittelpunkt. Für die Torsionskennwerte ergeben sich dann

Elastischer Nachweis für dünnwandige Querschnitte
Der elastische Nachweis kann für alle dünnwandigen Querschnitte durchgeführt werden,
die entweder der pcae-Profiltafel entnommen, parametrisiert eingegeben oder mit dem
pcae-Programm 4H-QUER als dünnwandiges Profil erzeugt wurden.
Flach- und Rundstähle sind jedoch vom Nachweis ebenso ausgenommen wie dickwandige
4H-QUER-Querschnitte.
Einen dünnwandigen Querschnitt kennzeichnet, dass seine Blechdicken im Verhältnis zu ihrer Länge klein sind, sodass der Querschnitt über Linien modelliert werden kann.
Jede Linie hat eine ggf. linear veränderliche Dicke und kann Ausrundungen am Anfang und
Ende besitzen.
Der elastische Nachweis berücksichtigt sämtliche Schnittgrößen.
Die Normalspannungen werden am polygonalen Querschnitt berechnet, während die Schubspannungen auf die Linien bezogen werden. Demzufolge gilt für den Schubspannungsanteil der Querkräfte, dass die Schubspannungen in der grafischen Darstellung über die Dicke konstant verlaufen (hier: horizontale bzw. vertikale Konturengrenzen), während der Anteil aus primärer Torsion sich linear über die Dicke verändert.
Im Ergebnisausdruck werden der Ort und die Größe der zugehörigen Spannungen bezogen auf das Querschnittskoordinatensystem im Schwerpunkt protokolliert.
Der Nachweis wird für die maximale Vergleichsspannung geführt.
Beispiel U100
Elastischer Nachweis mit der Finite-Elemente-Methode
Dieser Nachweis wird für sämtliche Querschnittsformen und alle Schnittgrößen angeboten.
Es können dünnwandige, d.h. über ihre Profilmittellinie definierte (s.o.), und dickwandige, d.h. polygonal umrandete, Querschnitte berechnet werden.
Es werden Kennwerte für jeden Elementknoten ermittelt, die nur von der Querschnittsform
abhängen und daher nur einmal berechnet werden müssen. Die Spannungen in den Knoten
werden anschließend durch Multiplikation der Schnittgrößen mit den Kennwerten ermittelt.
Der Nachweis berücksichtigt sämtliche Schnittgrößen.
Die lineare Normalspannungsverteilung wird aus Querschnittsfläche und Trägheitsmomenten berechnet.
Die Ermittlung der Schubspannung erfolgt auch für dünnwandige Querschnitte nach der 'dickwandigen' Theorie.
Die genauere Erfassung der Schubspannungen aus Querkraft in den Ausrundungsbereichen und Ecken im Vergleich zur Berechnung dünnwandiger Querschnitte (s.o.) ist in der grafischen Darstellung gut zu erkennen.
Im Ergebnisausdruck werden die Verläufe der Dehnungen, Spannungen und Ausnutzung als Konturenplot dargestellt.
Eine Tabelle zeigt den Ort und die Größe der zur maximalen Ausnutzung gehörenden Größen; Maximalwerte
werden gelb unterlegt. Der Nachweis wird für die maximale Vergleichsspannung geführt.
Beispiel U100
Elastischer Nachweis mit der Spannungsebene
Dieser Nachweis berücksichtigt nur Normalkraft und Biegemomente und wird für sämtliche Querschnittsformen angeboten.
Aus den Querschnittsgrößen Fläche und Trägheitsmomente werden mit Hilfe der Spannungsebene die Querschnittspunkte mit der maximalen und minimalen Normalspannung ermittelt.
Da die Bernoulli-Hypothese vom Ebenbleiben der Querschnitte gilt, liegen die Normalspannungen auf einer
Ebene, die um die Spannungsnulllinie als Achse dreht.
Die Querschnittsfasern mit den größten Abständen beidseitig der Nulllinie erhalten die größte (positive)
und die kleinste (negative) Spannung.
Die Gleichung der Normalspannung lautet
wobei sowohl die Biegemomente My, Mz als auch die Trägheitsmomente Iy, Iz, Iyz auf das Querschnittskoordinatensystem bezogen sind.
Im Ergebnisausdruck werden der Ort und die Größe der extremalen Spannungen bezogen auf das Querschnittskoordinatensystem im Schwerpunkt protokolliert.
Der Nachweis wird für die betragsmäßig größte Normalspannung geführt.
Beispiel U100
Plastischer Nachweis nach der Methode mit Teilschnittgrößen
Der Nachweis kann für dünnwandige Dreiblechquerschnitte (I-, C-, U-, Z-, L-, T-Querschnitte) durchgeführt werden,
die entweder der pcae-Profiltafel entnommen oder parametrisiert eingegeben wurden.
4H-QUER-Querschnitte sind generell ausgenommen.
Dieser Nachweis ist der bevorzugte plastische Nachweis für die pcae-Programme und wird für sämtliche Schnittgrößen angeboten.
Das Teilschnittgrößenverfahren (TSV) mit Umlagerung wurde von R. Kindmann, J. Frickel: Elastische und
plastische Querschnittstragfähigkeit entwickelt. Es wird überprüft, ob die Schnittgrößen vom Querschnitt unter
Ausnutzung der plastischen Reserven aufgenommen werden können (plastische Querschnittstragfähigkeit).
Dazu wird zunächst die schubspannungserzeugende Belastung auf die Einzelbleche aufgebracht, die dadurch eine verminderte Aufnahmekapazität erhalten. Anschließend wird ein Gleichgewichtszustand für die normalspannungs-erzeugende Belastung und die verbleibende Tragfähigkeit der Bleche gesucht.
Die Ausnutzung des Gesamtquerschnitts entspricht dem Kehrwert des Laststeigerungsfaktors.
Beispiel U100
Plastischer Nachweis nach der Methode mit Dehnungsiteration
Der Nachweis kann für alle dünnwandigen Querschnitte durchgeführt werden, die entweder der pcae-Profiltafel entnommen, parametrisiert eingegeben oder mit dem pcae-Programm 4H-QUER als dünnwandiges Profil
erzeugt wurden.
Flach- und Rundstähle sind jedoch ebenso ausgenommen wie dickwandige 4H-QUER-Querschnitte.
Das Verfahren der Dehnungsiteration (DIV) wird in R. Kindmann, J. Frickel: Elastische und plastische Querschnittstragfähigkeit (Kapitel 10.10) beschrieben.
Ähnlich wie beim Teilschnittgrößenverfahren werden die Schubspannungen aus Querkraft und Torsion der einzelnen Querschnittsteile (Flansche, Stege, ...) aus der elastischen Schubverteilung berechnet. Diese Schubspannungen reduzieren die zulässige Normalspannung der Teile.
Können die Schubspannungen nicht aufgenommen werden, muss der maximal mögliche Lastfaktor reduziert werden.
Die Schubspannungen werden bei Spannungsüberschreitungen nicht umgelagert.
Die Verwölbung der Querschnittsteile wird wie beim elastischen Verfahren für dünnwandige Querschnitte ermittelt
und in den einzelnen Teilen als ebene Verformung angesetzt.
Durch Variation der Dehnungsebene und der Verdrillungsableitung wird unter Berücksichtigung der reduzierten zulässigen Normalspannungen ein Dehnungszustand gesucht, dessen resultierende Schnittgrößen ein maximales Vielfaches der aufzunehmenden Schnittgrößen sind.
Dieser Grenzdehnungszustand darf für keinen Querschnittspunkt die Bruchdehnung εu überschreiten
bzw. -εu unterschreiten.
Falls der sich so ergebende maximale Lastfaktor evtl. nicht mit dem für die Schubspannungen verwendeten
Lastfaktor übereinstimmt, sind weitere Berechnungsschritte notwendig, bis die Lastfaktoren nahezu gleich sind.
Die plastische Querschnittsausnutzung ist der Kehrwert des maximalen Lastfaktors.
Es ist zu beachten, dass abhängig von der Querschnittsform, auch Lastkombinationen ohne Wölbschnittgrößen im Grenzzustand zu einer Verwölbung des Querschnitts führen können. Eine Vernachlässigung des Wölbgleichgewichts ergibt eine geringere Ausnutzung.
Beispiel U100
Plastischer Nachweis nach EC 3-1-1, 6.2
Dieser Nachweis wird nur für das Doppel-T-Profil, das Hohlprofil und den Flachstahl angeboten.
4H-QUER-Querschnitte sind generell ausgenommen.
Der Nachweis wird für alle Schnittgrößen mit Ausnahme der Verwölbungsgrößen Tω und B angeboten.
Er folgt den Regeln des EC 3-1-1, 6.2.2 bis 6.2.10. Es wird der ungeschwächte Bruttoquerschnitt zu Grunde gelegt.
Der Querschnitt gehört den Klassen 1 oder 2 an.
Die plastische Normalkrafttragfähigkeit berechnet sich mit (6.2.3+4)
Die plastische Biegetragfähigkeit berechnet sich mit (6.2.5)
Die plastische Querkrafttragfähigkeit berechnet sich mit (6.2.6)
Die plastische Torsionstragfähigkeit berechnet sich mit (6.2.7)
Die plastische Berechnung basiert auf dem Nachweis der Momentenbeanspruchbarkeit. Dazu wird die plastische Biegetragfähigkeit in Abhängigkeit der anderen Beanspruchungen (N, V, T) abgemindert.
Bei kombinierter Beanspruchung aus Querkraft und Torsion ergibt sich nach 6.2.7
Die ggf. abgeminderte Querkraft wirkt sich nach 6.2.8 auf die Momententragfähigkeit aus, wenn gilt
Anstelle der Steifigkeit fy wird das plastische Widerstandsmoment um den ρ-Anteil der querkraftbelasteten Querschnittsteile reduziert. Dadurch ergibt sich die reduzierte plastische Biegetragfähigkeit zu
Die gleichzeitige Wirkung einer Normalkraft ist nach 6.2.9 bei der Biegetragfähigkeit zu berücksichtigen, wenn gilt
Die reduzierte Biegetragfähigkeit beträgt
wobei die Biegetragfähigkeit bereits durch Querkraft und/oder Torsion abgemindert sein kann.
Ebenso kann die Normalkrafttragfähigkeit durch Querkraft und/oder Torsion abgemindert sein, da die querkraftbeanspruchten Querschnittsteile um den Faktor ρ reduziert werden.
Der Nachweis wird bei einachsiger Biegung mit Normalkraft geführt mit
und bei zweiachsiger Biegung mit Normalkraft mit
Beispiel Blech 50 x 8.5
Das Programm 4H-EC3QN weist Bauteile aus Aluminium elastisch nach.
Beulen ist ausgeschlossen, d.h. der Querschnitt befindet sich mindestens in Querschnittsklasse 3
(s. EC 9-1-1, 6.1.4.4).
Der Spannungsnachweis eines Aluminium-Querschnitts erfolgt mit dem Fließkriterium nach EC 9-1-1, 6.2.1(5).
Der Sicherheitsbeiwert beträgt nach EC 9-1-1, 6.1.3(1) γM1 = 1.1 (s. ggf. EC 9-1-1, NA).
Die zulässige Fließgrenze entspricht der 0.2%-Dehngrenze fo der jeweiligen Legierung.
Die zulässige Vergleichsspannung darf um den Faktor C0.5 = 1.200.5 = 1.095 (s. ggf. EC 9-1-1, NA) erhöht werden, wohingegen die Normal- und Schubspannungen ohne Erhöhung der zulässigen Spannungen nachgewiesen werden.
Die Dehnungen in der Ergebnisausgabe werden mit der materialspezifischen Spannungs-Dehnungs-Beziehung für Traglastnachweise (s. Ramberg-Osgood-Modell in EC 9-1-1, E.2.2.2) aus den Normalspannungen berechnet.
Der Exponent n ist abhängig vom Dehnungsbereich, der dem untersuchten Verhalten entspricht. Wenn die
Berechnung elastisch erfolgt, wird n mit Gl. (E.15) ermittelt, bei plastischer Berechnung wird Gl. (E.18) angewandt.
Aktuell wird für Aluminiumlegierungen nur der elastische Nachweis angeboten. Daher erfolgt die Berechnung des Exponenten mit (E.15).
Die Auswirkungen der exponentiellen Zunahme der Dehnungen bei hoher Beanspruchung werden im Deformationsplot deutlich. Beispielhaft wird ein Aluminiumprofil diagonal durch ein Moment belastet. Die Ausnutzung in den diagonal gegenüberliegenden Ecken ist überschritten, d.h. dass die Normalspannungen größer als die 0.2%-Dehngrenze sind.
Die Berechnung der Dehnungen nach dem Hooke'schen Gesetz (ε = σ / E) erzeugt eine Dehnungsebene
(gleichmäßig eben), während die Dehnungen bei der Berechnung nach EC 9, Anhang E in den Bereichen,
in denen die 0.2%-Dehngrenze der Spannungen überschritten wird, sich nichtlinear verhalten.
Das Programm bietet drei elastische und drei plastische Verfahren an, einen Querschnitt zu bemessen.
Die Verfahren unterscheiden sich i.W. in ihrer Anwendbarkeit auf verschiedene Querschnittstypen. Nähere Informationen zu den Verfahren finden Sie hier.
In der Literatur werden bevorzugt Verfahren entwickelt, die nur für häufig vorkommende Querschnittstypen gelten.
Anhand des Doppel-T-Profils werden im Folgenden die Unterschiede der Verfahren dargestellt (Bsp. 1).
Anschließend wird die Berechnung von frei definierten Querschnitten (s. 4H-QUER) aus Aluminium vorgestellt
und der Unterschied zum Material Stahl erläutert (Bsp. 2).
Zum Schluss werden die Auswirkungen der Wölbkrafttorsion dargestellt (Bsp. 3). Beachte: Die Spannungen
treten bei Behinderung der Verwölbung auf, also maßgeblich bei Verbindungen.
Bsp. 1 - Wagenknecht, 2.6.1: HE300A, S235, My,Ed = 225 kNm, Vz,Ed = 160 kN
Elastische Spannungsnachweise
Die elastischen Spannungsnachweise berechnen die Normalspannungen generell mit
(s. Querschnittsnachweise), wobei für diesen Querschnittstyp Iη = Iy und Iζ = Iz .gelten
Die Querschnittsparameter werden aus den Profilparametern berechnet und können daher geringfügig von Tabellenwerten abweichen.
Abweichungen zwischen den Nachweisen ergeben sich vor allem in der Berechnung der Schubspannungen.
Die maximale Tragfähigkeit wird in Wagenknecht mit U = 0.73 am Steganschnitt angegeben.
dünnwandiger Querschnitt
Bei diesem Verfahren wird der Querschnitt durch seine Mittellinien und die zugehörigen Blechdicken beschrieben. Ausrundungen und veränderliche Blechdicken werden berücksichtigt.
Die extremalen Normalspannungen beziehen sich auf die äußersten Querschnittsfasern (nicht auf die Mittellinien!), wohingegen die Schubspannungen für die Mittellinien berechnet werden.
Zu jeder extremalen Größe werden die Querschnittskoordinaten y,z bezogen auf den Schwerpunkt und die
zugehörigen Spannungen σx, τ, σv angegeben.
Der Nachweis wird für die maximale Vergleichsspannung geführt und ergibt die Tragfähigkeit (Ausnutzung U).
Die maximale Vergleichsspannung und damit auch die maximale Ausnutzung tritt im Flansch bei
z = ± 138 mm = h/2 - tf/2 auf, also im Schnittpunkt der Mittellinien.
Bei diesem Verfahren ist der Konturenplot verfügbar, er zeigt die Spannungsverteilung an. Die Normalspannungen werden farblich markiert, hier steht rot für Druck und blau für Zug (Palette 1).
Die Schubspannungen sind stets positiv, daher ist die Konturdarstellung neutral gehalten. Die Intensität der Farben zeigt die Größe des Ergebniswerts an.
Deutlich zu erkennen ist der lineare Verlauf der Normalspannungen. Es wird programmintern dafür gesorgt,
dass sich die neutrale Zone im hellsten Farbbereich (Palette 1) befindet.
Die Schubspannungen sind senkrecht zur Mittellinie konstant. In den Knotenpunkten (Flansche-Steg) ergeben sich sprunghafte Veränderungen, die auf das Verfahren zurückzuführen sind. Der Maximalwert tritt in Stegmitte auf.
Die Konturenergebnisse können zudem tabellarisch dargestellt werden. I.A. werden nur die extremalen Werte ausgegeben, die führenden Werte ±ε, ±σx, τ, σv sind unterlegt.
Die maximale Ausnutzung berechnet sich nach dieser Methode zu U = 0.86, liegt also im Vergleich zur
Handrechnung (Wagenknecht) auf der sicheren Seite.
Finite-Elemente-Methode
Der Querschnitt wird polygonal modelliert und mit FEM ganzheitlich berechnet, d.h. vorab berechnete Querschnittsparameter sind nicht von Belang.
Der Q. wird unter Berücksichtigung der Schlankheit seiner Bleche diskretisiert. Die Netzdichte kann beeinflusst werden, wenn der Profi-Button aktiviert ist.
Aus den Ergebnissen in den Knotenpunkten werden die extremalen Dehnungen, Spannungen und Ausnutzungen ermittelt und in einer Tabelle dargestellt.
Bei diesem Verfahren ist der Konturenplot obligatorisch (Erläuterung s.o. 'dünnwandiger Querschnitt').
Die Schubspannungen ergeben sich nach diesem Verfahren veränderlich über die Blechdicke. Der Knotenbereich
von Flanschen und Steg ist gegenüber dem Verfahren der dünnwandigen Querschnitte besser erfasst. Dadurch
ergibt sich ein realitätsnäheres Ergebnis.
Aus der Ergebnistabelle lässt sich ablesen, dass die maximale Tragfähigkeit an der Flanschaußenkante
im Bereich des Stegs auftritt.
Die maximale Ausnutzung berechnet sich nach dieser Methode zu U = 0.77; größer als der Wert der Handrechnung (Wagenknecht). Der Grund liegt darin, dass dieses Verfahren die äußerste Querschnittsfaser berücksichtigt, Wagenknecht die Normalspannungen nach EC 3-1-1 in Flanschmitte berechnet.
Die FEM berechnet dort eine maximale Ausnutzung von U = 0.74, was in etwa der Ausnutzung am
Steganschnitt entspricht.
Die FEM ist genauer als das Verfahren für dünnwandige Querschnitte, jedoch erfordert es bei komplexen Querschnitten (s. Bsp. 3) erheblich mehr Rechenzeit.
Spannungsebene
Das Verfahren ist ein Handrechenverfahren zur Berechnung von normal- und biegebelasteten Querschnitten.
Schubkräfte (Querkraft und Torsion) können nicht nachgewiesen werden.
Es wird die Gleichung der Spannungsebene und der Spannungsnulllinie (neutrale Faser) protokolliert. Daraus
berechnen sich die extremalen Normalspannungen, die sich auf die äußersten Querschnittsfasern beziehen.
Zu jeder extremalen Größe werden die Querschnittskoordinaten y,z bezogen auf den Schwerpunkt und die
zugehörigen Spannungen σx angegeben.
Der Nachweis wird für die Bemessungsnormalspannung geführt und ergibt die Tragfähigkeit (Ausnutzung Uσ = 0.76).
 
Plastische Spannungsnachweise
Nachweis mit Teilschnittgrößen (TSV)
Der Nachweis ist anwendbar für offene, dünnwandige Zwei-/Drei-Blech-Querschnitte aus der pcae-Profildatenbank.
Frei definierte Querschnitte (4H-QUER) können nicht nachgewiesen werden.
Für die Einzelbleche (Obergurt, Untergurt, Steg) werden die Grenzkräfte berechnet und die anteiligen Schnittgrößen nachgewiesen. Die Gesamtausnutzung kann jedoch auf Grund der Spannungsumlagerungen nur durch Laststeigerung berechnet werden.
Daraus ergibt sich für das gewählte Beispiel eine Ausnutzung von U = 0.75; für dieses Beispiel nur geringfügig kleiner als die elastische Querschnittsausnutzung.
Die Ergebnisse können nicht als Konturenplot dargestellt werden.
Methode mit Dehnungsiteration (DIV)
Der Nachweis kann für alle dünnwandigen Querschnitte (pcae-Profilmanager, parametrisiert, 4H-QUER - dünnwandig) geführt werden.
Der Querschnitt wird durch seine Mittellinien beschrieben. Iterativ wird der plastische Grenzdehnungszustand des Querschnitts unter der gegebenen Lastkombination für ε = ± 150 ‰ ermittelt.
Die Grenzdehnungen können modifiziert werden, wenn der Profi-Button aktiviert ist. Außerdem kann festgelegt
werden, ob das Wölbgleichgewicht bei Berechnung des Grenzzustands eingehalten werden soll.
Die Querschnittsausnutzung beträgt hier nur U = 0.72.
Die Ergebnisse der plastischen Berechnung können im Konturenplot visualisiert werden. Es werden jedoch lediglich die Grenzdehnungen, Grenzspannungen und die lokale Ausnutzung dargestellt. Es lässt sich also nicht der aktuelle Plastizierungsgrad ablesen.
Die Grenznormalspannungen sind unter der gegebenen Lastkombination konstant bis zur Querschnittsachse und erreichen den Grenzwert σx = ± 234 N/mm2.
Die Querkraft wird allein vom Steg aufgenommen und bewirkt eine maximale Grenzschubspannung von
max τ = 84 N/mm2.
Daraus ergeben sich die Grenzvergleichsspannungen, die in nahezu allen Querschnittspunkten der Grenzspannung
fyd = 235 N/mm2 entsprechen, d.h. der Querschnitt ist optimal plastisch nachgewiesen.
In der Ergebnistabelle werden die o.a. Werte zahlenmäßig ausgegeben.
Die maximale Ausnutzung bezieht sich bei plastischer Berechnung auf den Gesamtquerschnitt und berechnet
sich nach dieser Methode zu U = 0.72.
Das Verfahren mit Dehnungsiteration ist flexibler als das Verfahren mit Teilschnittgrößen, da es beliebige
dünnwandige Querschnitte plastisch berechnet. Allerdings geht die Flexibilität einher mit einer erheblich
längeren Rechenzeit.
Nachweis nach EC 3-1-1, 6.2
Der Nachweis ist nur für wenige Querschnittstypen, Doppel-T- und dünnwandige Hohlprofile, verfügbar.
4H-QUER-Querschnitte können nicht nachgewiesen werden. Wölbkrafttorsion ist ausgeschlossen.
Es werden die Eurocode-Formeln für den plastischen Querschnittsnachweis angewandt. Nachvollziehbar wird jeder Rechenschritt dargestellt, bis die abgeminderte plastische Momententragfähigkeit bestimmt ist.
Für dieses Beispiel ergibt sich damit eine geringe Ausnutzung von U = 0.70, da nach Norm die Querkraft die Momententragfähigkeit nicht beeinflusst.
Das genauere Verfahren (DIV) bescheinigt jedoch einen, wenn auch geringen, Einfluss der Schubspannung
auf die Querschnittsausnutzung.
Die Ergebnisse können nicht als Konturenplot dargestellt werden.
Bsp. 2 - 4H-QUER-Querschnitt (Laufs/Radlbeck A.2), 4H-QUER-Profil, Aluminium 6060 T6 mit t ≤ 15 mm,
N = -4.3 kN, Mz,Ed = 6.59 kNm, Vy,Ed = 3.77 kN
Der Pfosten einer Aluminium-Glasfassade ist zu bemessen. Er wird mit dem Programm 4H-QUER modelliert;
einerseits über die Mittellinien seiner Bleche (Typ: dünnwandig), andererseits polygonal (Typ: dickwandig).
Die Beschreibung des dünnwandigen Querschnitts erfolgt über die Mittellinien der Bleche und ihre Dicken.
Die Koordinaten der Knotenpunkte und die zugeordneten Linien können als zusätzliche Information
protokolliert werden.
Schwerpunkt und Schubmittelpunkt sind markiert.
Die Beschreibung des dickwandigen Querschnitts erfolgt über die Knotenpunkte der Außenberandung und der Aussparungen. In einer Tabelle werden die Koordinaten bezogen auf den Ursprung yp/zp angegeben.
Schwerpunkt und Schubmittelpunkt sind markiert.
Die Berechnung erfolgt mit der Finite-Elemente-Methode, die Ergebnisse werden anschaulich in der Konturendarstellung visualisiert.
Normalspannungen und Schubspannungen werden zu Vergleichsspannungen zusammengefasst, jeder
Spannungstyp jedoch einzeln nachgewiesen.
Es ergibt sich eine maximale Ausnutzung, die bei Aluminium im Unterschied zu Stahl nicht unbedingt direkt
aus der Vergleichsspannung hervorgeht.
Die maßgebenden Nachweise werden protokolliert.
Bsp. 3 - IPE 300, S235, My = 60.6 kNm, Vz 41.4 kN, Tt = 1.7 kNm, Tω = 2.3 kNm, B = 2.4 kNm2
Ein Träger IPE 300 erhält Schnittgrößen aus Torsion. Da dieser Querschnitt wölbempfindlich ist, werden zusätzlich
zur St. Venant'schen Torsion Tt Wölbschnittgrößen Tω und B angesetzt.
Der elastische Spannungsnachweis (FEM) zeigt eine deutliche Spannungsüberschreitung (Ausnutzung U = 1.41 > 1), während der plastische Spannungsnachweis (DIV) mit U = 0.93 gelingt.
Es ist zu beachten, dass beim plastischen Nachweis das Wölbgleichgewicht eingehalten wird.
Da sich eine Einhaltung des Gleichgewichts in der fachlichen Diskussion befindet und ggf. nicht zwingend
erforderlich ist, kann die Berechnung auch ohne Einhaltung durchgeführt werden. Dazu ist der Profi-Button zu aktivieren und die entsprechende Option auszuwählen.
Das Ergebnis zeigt nun eine wesentlich geringere plastische Ausnutzung (U = 0.71), wobei das Gleichgewicht
(s. ΔB) nicht eingehalten wird.
Bei elastischer Nachweisführung werden die Daten für die Visualisierung der Dehnungen als Deformationsplot erzeugt. Im Ergebnis-Darstellungsfenster ist die Verwölbung des Querschnitts bzgl. seiner Längsachse gut zu erkennen.
zur Hauptseite 4H-EC3QN, Querschnittsnachweis