 |
|
| Seite überarbeitet März 2024 |
 |
Kontakt |
 |
|
 |
Programmübersicht |
 |
|
 |
Bestelltext |
 |
|
|
| Infos auf dieser Seite |
... als pdf |
 |
|
 |
 |
Anschlussparameter ............... |
 |
|
 |
Schweißnahtnachweis DIN ..... |
 |
|
Basisverbindungen |
 |
Schnittgrößen ........................ |
 |
|
 |
Querschnittsnachweis DIN ..... |
 |
|
 |
Schweißverbindungen ............ |
 |
|
 |
Schnittgrößenimport ............ |
 |
|
 |
Theorie dünnwandiger Quer. |
 |
|
 |
Stahlsorten ........................... |
 |
|
 |
Schweißnahtnachweis EC 3 ... |
 |
|
 |
Ergebnisse dünnw. Querschn. |
 |
|
 |
Ausdrucksteuerung ................ |
 |
|
 |
Querschnittsnachweis EC 3 ... |
 |
|
 |
Ergebnisübersicht ................. |
 |
|
 |
nationale EC-Anhänge ............ |
 |
|
|
|
|
 |
|
 |
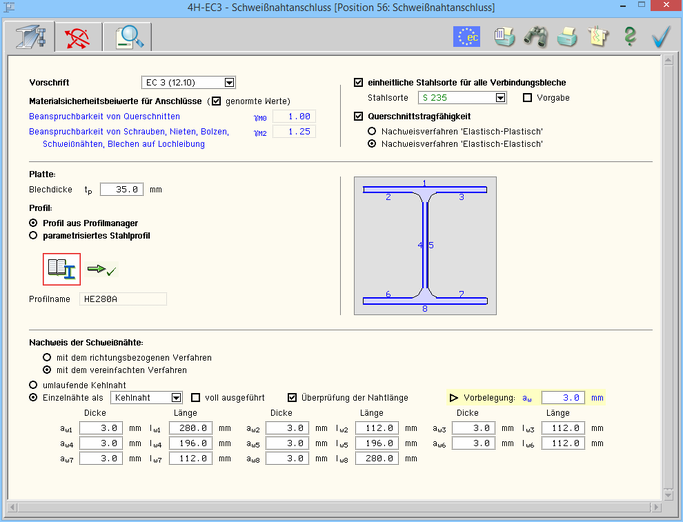
Register 1 enthält Angaben zu
den Anschluss- und Materialparametern |
|
|
 |
|
| Bild vergrößern |
 |
|
|
|
| Allgemeines |
 |
|
| Das Programm 4H-EC3SA berechnet den geschweißten
Anschluss eines typisierten Profils an eine Stahlplatte. |
|
Der Nachweis kann nach EC 3-1-8
oder
DIN 18800 (veraltet) erfolgen. |
| Dementsprechend sind
die Material-sicherheitsbeiwerte zu belegen. |
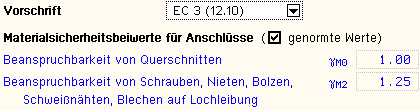
| Nach EC 3 können die Sicherheitsbeiwerte entweder
dem nationalen
Anhang entnommen oder direkt
vorgegeben werden. |
|
 |
|
Nach DIN 18800 ist der Sicherheitsbeiwert
in das Eigenschaftsblatt einzutragen. |
|
 |
|
|
|
| Export / Import |
 |
|
| Die Eingabedaten können über die Copy-Paste-Funktion
von einem Bauteil in ein anderes derselben Programmfamilie (4H-EC3SA) übertragen
werden. |
|
|
|
|
Dazu ist der aktuelle Datenzustand im abgebenden Bauteil über
den Button Daten exportieren in die
Zwischenablage zu kopieren und anschließend über den Button Daten
importieren in das aktuell geöffnete
Bauteil aus der Zwischenablage zu übernehmen. |
|
| Material |
 |
|
| Grundsätzlich kann jedem Verbindungselement
ein eigenes Material zugeordnet werden. |
|
| Der Übersichtlichkeit halber kann
an dieser Stelle eine einheitliche Stahlgüte für
Profil und Platte
gewählt werden. |
|
 |
|
|
| Da die Beschreibung der Stahlparameter für
Verbindungen nach EC 3 programmübergreifend identisch ist,
wird auf die allgemeine
Beschreibung der Stahlsorten verwiesen. |
|
|
| Platte |
 |
|
|
| Mit Platte wird das Bauteil bezeichnet,
an das das Profil angeschweißt wird. |
| Lediglich
die Plattendicke ist für den Nachweis von Relevanz. |
|
 |
|
|
| Profil |
 |
|
Die Profilkennwerte können entweder
über den
pcae-eigenen Profilmanager in das Programm
importiert oder als
parametrisiertes
Stahlprofil eingegeben werden. |
| Der Nachweis
nach DIN 18800 ist für
parametrisierte Profile nicht möglich. |
|
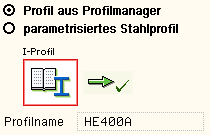
Um ein Profil aus dem Angebot des Profilmanagers zu
wählen,
ist der grün unterlegte Pfeil zu anzuklicken. |
Das externe
pcae-Programm wird aufgerufen und ein Profil
kann
aktiviert werden. Bei Verlassen des Profilmanagers werden die
benötigten Daten übernommen und der Profilname protokolliert. |
|
 |
|
|
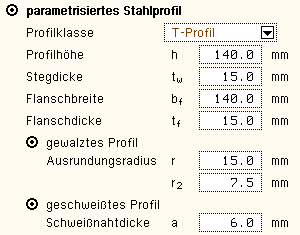
Zur Definition eines parametrisierten
Profils (nur EC 3) sind
neben der Profilklasse
die Profilhöhe,
Stegdicke, Flanschbreite
und -dicke festzulegen. |
Bei gewalzten Profilen wird der Ausrundungsradius
r zwischen Flansch und Steg bzw. r2 an den äußeren Flanschrändern
geometrisch berücksichtigt,
während geschweißte Blechprofile
mit Schweißnähten
der Dicke a zusammengefügt sind. |
| Diese Schweißnähte werden nicht nachgewiesen. |
|
Das Profil wird maßstabsgetreu am Bildschirm
dargestellt,
wobei die Neigung von Flanschen oder Steg
nicht berücksichtigt werden. |
|
 |
|
|
|
| Schweißnähte |
 |
|
| Die Schweißverbindung kann als umlaufende Kehlnaht
oder durch Einzelnähte ausführt werden. |
|
 |
|
|
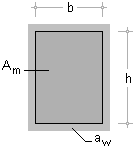
| Die umlaufende Kehlnaht mit
einer konstanten Nahtdicke aw wird in einer maßstäblichen
Grafik am Bildschirm dargestellt. |
Bei dieser Schweißart besteht die Möglichkeit,
den Anteil der Normalkraft, der
über Druckkontakt
abgetragen wird und demnach die Schweißnaht nicht belastet,
zu bestimmen. |
|
 |
|
|
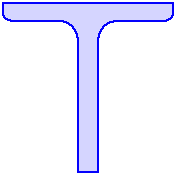
| Einzelnähte können
entweder als Kehlnaht oder als nicht durchgeschweißte
Stumpfnaht (HY-Naht, nur
EC 3) ausgeführt
werden. |
| Am Bildschirm wird in einer maßstäblichen
Grafik sowohl die Nahtart farblich gekennzeichnet (Kehlnaht
blau, Stumpfnaht braun) als auch die Nummer der Naht
angegeben. |
Einzelnähte verlaufen grundsätzlich
entlang der Flansch- bzw. Stegdicken und
nicht an Rundungen. |
| Für alle Einzelnähte
gilt, dass Kehlnähte entweder voll ausgeführt
(d.h. rechnerisch in ihrer gesamten Länge angesetzt)
oder mit Endkrater versehen sein können. |
Die Nahtlänge
kann vor der Berechnung überprüft
und die Naht ggf. nicht wirksam werden (nur
EC 3). |
| Für alle Nähte
sind Nahtdicke aw und
Nahtlänge lw anzugeben. |
|
 |
|
| Ist die Nahtdicke
aw = 0, wird keine Schweißnaht angesetzt. |
Bei nicht durchgeschweißten
Stumpfnähten
darf die Nahtdicke aw den Maximalwert von
(t - 3 mm)/2
nicht überschreiten. |
Die Eingabe einer Nahlänge lw = 0 führt
dazu, dass die Nahtlänge an der entsprechenden Bauteilkante
bei der Berechnung in voller Länge angesetzt wird. Eine Reduktion
aufgrund von Endkraterausbildung bei Kehlnähten
ist jedoch möglich. |
|
| Optional können Blech- und Nahtdicke überprüft
werden (nur EC 3). Ist der Schalter deaktiviert, wird weder die Unter-
noch die Überschreitung
der zulässigen Grenzwerte von Blech- und Nahtdicke gemeldet. |
|
Bei Änderung des Profiltyps (Profilmanager oder parametrisiert),
bei Auswahl eines neuen Profils aus dem Profilmanager oder bei Bestimmung einer
neuen Profilklasse des parametrisierten Stahlprofils werden die
Nahtlängen mit Maximalwerten vorbelegt. |
Die Schweißnahtdicken können über den
Aktionsbutton  mit
der blau dargestellten Größe
einheitlich belegt mit
der blau dargestellten Größe
einheitlich belegt
werden, wobei nur 'vorhandene' Schweißnähte, d.h.
Nähte mit aw > 0, überschrieben werden. |
|
| Nachweise |
 |
|
Die Schweißnähte können
mit dem richtungsbezogenen oder dem vereinfachten
Verfahren (nur EC 3)
nachgewiesen werden. Optional kann auch die Ausnutzung
des Querschnitts ermittelt werden. |
| Außerdem ist das Verfahren zur
Aufteilung der Querkräfte auf die Schweißnähte festzulegen (nur
EC 3). |
|
| Zur Beschreibung der Nachweise nach EC 3. |
| Zur Beschreibung der Nachweise nach DIN 18800. |
|
|
|
|
|
|
 |
| |
 |
das zweite Register beinhaltet die
Masken zur Eingabe der Bemessungsschnittgrößen |
|
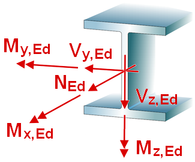
Die Schnittgrößen werden als Bemessungsgrößen
mit der Vorzeichendefinition
der Statik eingegeben, wobei das x,y,z-Koordinatensystem
dem l,m,n-System
der
pcae-Tragwerksprogramme entspricht. |
| Es können bis zu 10.000 Schnittgrößenkombinationen eingegeben werden. |
|
 |
Bei
Übernahme der Schnittgrößen aus einem Tragwerksprogramm ist
zu beachten, dass sie sich auch bei unsymmetrischen Querschnitts-profilen (z.B. L-Profil) auf das
Stab-Koordinatensystem
und nicht auf
das Hauptachsensystem (
pcae-Bezeichnung: ξ,η,ζ)
beziehen! |
|
|
|
|
|
|
 |
|
|
 |
|
| Im Standardfall |
|
 |
| bewirken die Schnittgrößenkombinationen
N,My,Vz eine Biegung um die starke
Achse des Querschnitts |
|
 |
| bewirken die Schnittgrößenkombinationen
N,Mz,Vy eine Biegung um die schwache
Achse des Querschnitts |
|
 |
| wird das Torsionsmoment Mx nur
für doppelt-symmetrische
Querschnitte relevant |
|
|
|
| Schnittgrößen importieren |
 |
Detailnachweisprogramme zur Bemessung von Anschlüssen (Träger/Stütze, Träger/Träger), Fußpunkten
(Stütze/Fundament) etc.
benötigen
Schnittgrößenkombinationen, die häufig von einem Tragwerksprogramm
zur Verfügung gestellt werden. |
| Dabei handelt es sich i.d.R. um
eine Vielzahl von Kombinationen, die im betrachteten
Bemessungsschnitt des übergeordneten Tragwerkprogramms vorliegen
und in das Anschlussprogramm übernommen werden sollen. |
|
| pcae stellt neben der 'per Hand'-Eingabe
zwei verschiedene Mechanismen zur Verfügung, um Schnittgrößen
in das vorliegende Programm zu integrieren. |
|
 |
|
 |
| Import aus einer Text-Datei |
|
| Die Schnittgrößenkombinationen können
aus einer Text-Datei im ASCII-Format eingelesen werden. |
| Die Datensätze müssen in der Text-Datei in
einer bestimmten Form vorliegen; der entsprechende Hinweis wird bei
Betätigen des Einlese-Buttons gegeben. |
| Anschließend wird der
Dateiname einschl. Pfad der entsprechenden Datei abgefragt. |
| Es werden sämtliche vorhandenen
Datensätze
eingelesen und in die Tabelle übernommen.
Bereits bestehende
Tabellenzeilen bleiben erhalten. |
| Wenn keine Daten gelesen werden können, erfolgt eine entsprechende
Meldung am Bildschirm. |
|
|
| |
 |
| Import aus einem 4H-Programm |
|
| Voraussetzung zur Anwendung des DTE®-Import-Werkzeugs
ist, dass sich ein pcae-Programm
auf dem Rechner befindet, das Ergebnisdaten exportieren
kann. |
|
| Die statische Berechnung eines Bauteils beinhaltet
i.A. die Modellbildung mit anschließender Berechnung
des Tragsystems sowie nachfolgender Einzelnachweise
von Detailpunkten. |
| Bei der Beschreibung eines Details sind die zugehörenden
Schnittgrößen aus den Berechnungsergebnissen des Tragsystems zu extrahieren
und
dem Detailnachweis zuzuführen. |
|
| In der 4H-Programmorganisation gibt es hierzu verschiedene
Vorgehensweisen |
 |
zum einen können Tragwerks- und Detailprogramm
fest miteinander verbunden sein, d.h. die Schnittgrößenüber-
gabe
erfolgt intern. Es sind i.A. keine weiteren Eingaben
(z.B. Geometrie) notwendig, aber auch möglich (z.B.
weitere Belastungen), die Programme bilden eine Einheit. |
| Dies ist z.B. bei dem 4H-Programm Stütze
mit Fundament der Fall. |
|
 |
| zum anderen können Detailprogramme Schnittgrößen von in Tragwerksprogrammen speziell festgelegten Exportpunkten über ein zwischengeschaltetes Export/Import-Tool einlesen |
| Das folgende Beispiel eines einfachen Rahmens erläutert diesen 4H-Schnittgrößen-Export/Import. |
|
|
|
Zunächst sind im exportierenden 4H-Programm
(z.B. 4H-FRAP) die Stellen zu kennzeichnen,
deren Schnittgrößen beim nächsten Rechenlauf exportiert, d.h.
für
den Import bereitgestellt,
werden sollen. |
|
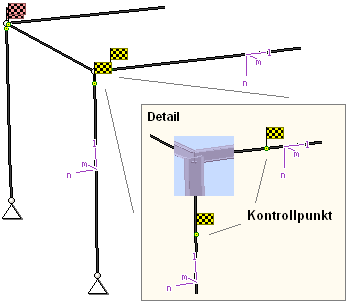
| In diesem Beispiel sollen die Schnittgrößen
für eine Querschnittsbemessung übergeben werden. |
Dazu
ist an der entsprechenden Stelle ein Kontroll-
punkt zu setzen. |
|
Ausführliche Informationen zum Export entnehmen
Sie
bitte dem DTE®-Schnittgrößenexport. |
Nach einer Neuberechnung des Rahmens stehen
die Exportschnittgrößen
dem aufnehmenden
4H-Programm (z.B. 4H-BETON, 4H-EC3SA,
4H-EC3BT, 4H-EC3RE,
4H-EC3GT, 4H-EC3TT
etc.) zum Import zur Verfügung. |
|
 |
|
|
 |
aus dem aufnehmenden 4H-Programm
wird nun über den Import-Button das
Fenster zur
DTE®-Bauteilauswahl aufgerufen.
Hier werden alle berechneten Bauteile dargestellt, wobei diejenigen,
die Schnittgrößen
exportiert haben, dunkel gekennzeichnet sind. |
|
|
Das gewünschte Bauteil kann nun markiert und über
den bestätigen-Button ausgewählt
werden. Alternativ kann
durch Doppelklicken des Bauteils direkt in die DTE®-Schnittgrößenauswahl verzweigt
werden. |
|
 |
|
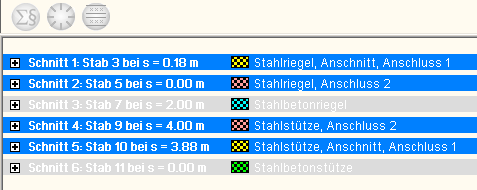
In der Schnittgrößenauswahl werden die verfügbaren
Schnittgrößenkombinationen aller im übergebenden
Programm gekennzeichneten Schnitte angeboten. Dabei sind diejenigen Schnitte
deaktiviert, deren Material nicht kompatibel
mit dem Detailprogramm ist. |
| Es wird nun der Schnitt angeklickt und damit geöffnet, dessen Schnittgrößen
eingelesen werden sollen. |
|
 |
|
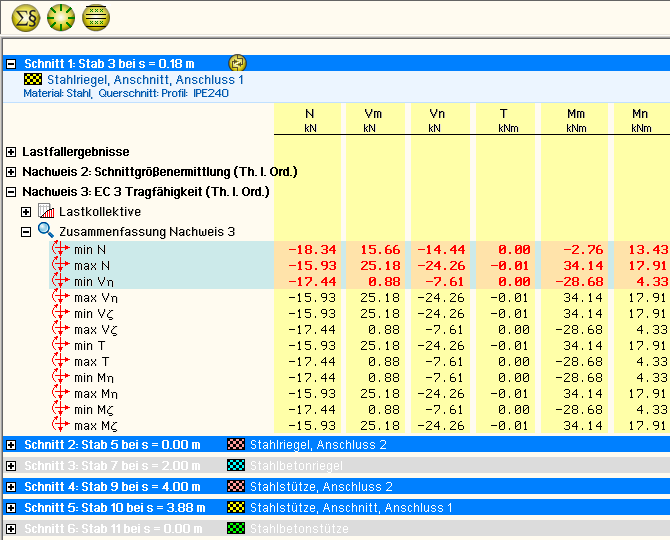
In 4H-EC3SA
ist der komplette verfügbare Schnittgrößensatz importierbar, was durch gelbe Hinterlegung der
Spalten angezeigt wird. |
| Die Schnittgrößenkombinationen können beliebig zusammengestellt
werden; pcae empfiehlt jedoch, nur diejenigen
auszuwählen, die als
Bemessungsgrößen für den zu führenden Detailnachweis
relevant sind. |
|
|
| ein nützliches Hilfsmittel
bietet dabei der dargestellte Button, mit dem die Anzahl zu übertragender Lastkombinationen durch Eliminierung doppelter Zeilen stark reduziert werden kann. |
|
|
|
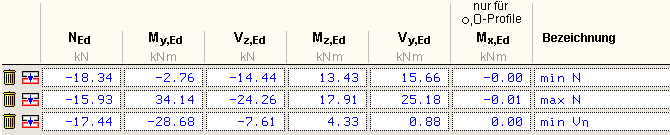
Wird nun die DTE®-Schnittgrößenauswahl bestätigt,
bestückt das Importprogramm die Schnittgrößentabelle,
wobei ggf. vorhandene Kombinationen erhalten bleiben. |
|
 |
|
Wenn eine Reihe von Anschlüssen gleichartig ausgeführt werden soll, können in einem Rutsch weitere Schnitt-
größen anderer Schnitte aktiviert und so bis zu 10.000 Kombinationen übertragen werden. |
|
|
| Die Kompatibilität der Querschnitts- und Nachweisparameter
zwischen exportierendem und importierendem Programm ist zu gewährleisten. |
|
|
| |
Eine Aktualisierung der importierten Schnittgrößenkombinationen, z.B. aufgrund einer Neuberechnung
des exportierenden Tragwerks, erfolgt nicht! |
|
|
|
|
|
|
|
|
|
 |
|
| I.A. werden die Verbindungselemente (Träger und
Stirnblech, Träger und Stütze, Stütze und Fußplatte)
mit Kehlnähten
verbunden, deren Schweißnaht konzentriert in der Wurzellinie
angenommen wird. Ebenso können (nicht durchgeschweißte) Stumpfnähte
verwendet werden, die hier als HY-Nähte berücksichtigt
werden. |
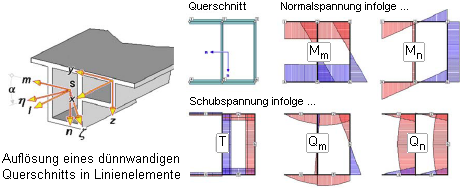
| Die Wurzellinien der Einzelnähte bilden den Linienquerschnitt
(s. G. Wagenknecht: Stahlbau-Praxis nach Eurocode 3, Band 2)
zur Aufnahme
bzw. Weiterleitung der Schnittgrößen. |
|
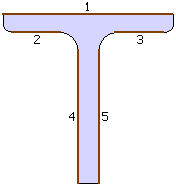
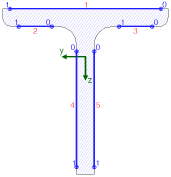
| Beispielhaft sind nebenstehend
die Einzelnähte,
die den Linienquerschnitt bilden, für einen
T-Querschnitt dargestellt. |
Die Nummerierung in rot kennzeichnet die
Naht,
die Zahlenangaben in blau
bezeichnen die maßgebenden
Nachweispunkte auf der jeweiligen Naht. |
Für jeden Punkt
einer Naht werden die Spannungen ermittelt und der Nachweis
geführt. |
| Zur Orientierung ist das Querschnitts-Koordinatenkreuz,
auf das die Schnittgrößen bezogen sind, in
grün eingefügt. |
|
 |
|
|
| Bei umlaufenden Nähten werden an jeder
gerade verlaufenden Profilkante Schweißnähte
angeordnet. |
| Diese haben im Normalfall eine einheitliche
Nahtdicke. |
| Es können Kehlnähte, nicht durchgeschweißte
und voll durchgeschweißte Stumpf-nähte angeordnet werden. |
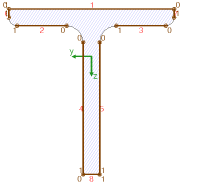
| Zur Unterscheidung werden Kehlnähte
in blau und Stumpfnähte in braun gezeichnet. Nebenstehend
ist der Linienquerschnitt einer umlaufenden Stumpfnaht
dargestellt. |
|
 |
|
|
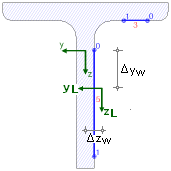
| Es ist zu unterscheiden zwischen
dem Querschnittsschwerpunkt und dem Schwerpunkt des Linienquerschnitts. |
Da die Einzelnähte beliebig lang und
dick sein können, kann der Schwerpunkt
des Linienquerschnitts
mehr oder weniger stark vom Querschnittsschwerpunkt abweichen. |
| Nebenstehend ist für
einen Extremfall das um Δyw und Δzw abweichende
Koordinatensystem
des Linienquerschnitts dargestellt. |
| |
|
 |
|
|
Bezogen auf den Schwerpunkt des Linienquerschnitts
werden die Querschnittsfläche
ΣAw,
ggf. die
Querschnittsflächen in y- und
z-Richtung Aw,y, Aw,z, die gesamte
Nahtlänge Σlw,
die Trägheitsmomente
Iw,y, Iw,z, Iw,yz und
die Differenzabstände zum Querschnittsschwerpunkt
Δ
yw, Δzw ermittelt. |
|
 |
|
| Über eine Interaktionsbeziehung (s. Theorie, mehrteilige Querschnitte) können
den Einzelnähten
Schnittgrößen zugeordnet werden, die im Schwerpunkt der
Naht wirken. |
| Die lokalen Normalkräfte und
Biegemomente werden
über diese Beziehung ermittelt. |
| Da die Querkraftaufteilung
unabhängig
von der Momenten-/Normalkraftverteilung erfolgt, werden zwei
Verfahren zur Verteilung der Querkräfte auf die Nähte
angeboten. |
 |
| nach der konventionellen Methode wird die Querkraft
denjenigen Nähten zugeordnet, die in Richtung der entsprechenden
Querkraftkomponente verlaufen, d.h. horizontale Nähte
tragen Vy, vertikale Nähte Vz. |
| Diese klassische Aufteilung wird beim
Schweißnahtnachweis nach DIN 18800 angewandt. |
|
|
|
 |
| alternativ wird die Querkraft in
Abhängigkeit der Steifigkeiten auf
die Nähte verteilt. |
| Dies entspricht der Theorie
der Aussteifungssysteme, die jedoch im strengen Sinne nur
gilt, wenn sich die Schweißnähte unabhängig
voneinander verformen können. |
|
|
|
|
| Damit werden die Spannungen in den maßgebenden
Nachweispunkten berechnet. |
|
| Sowohl Druck- als auch Zugnähte werden entweder
mit dem richtungsabhängigen |
|
| oder dem vereinfachten Verfahren nachgewiesen. |
|
Da die Beschreibung der Schweißnahtnachweise
nach EC 3 programmübergreifend identisch ist, wird auf die
allgemeine Beschreibung des Schweißnahtnachweises verwiesen. |
|
| Besonderheiten bei doppelt-symmetrischen Querschnitten mit
umlaufenden Kehlnähten |
|
| Zu den doppelt-symmetrischen Querschnitten im Sinne des Schweißnahtnachweises
zählen das Rohr- und Rechteckprofil sowie der Rundstahl, die
umlaufend geschweißt sind. |
| Sie sind in der Lage, zusätzlich zu den Normal-, Querkräften
und Biegemomenten auch Torsionsmomente aufzunehmen. |
|
|
 |
|
Der Tragsicherheitsnachweis der offenen, dünnwandigen
Querschnitte kann nach dem Nachweisverfahren
Elastisch-Elastisch (DIN
EN 1993-1-1, Abs. 6.2.1(5)) oder nach dem Nachweisverfahren Elastisch-Plastisch
geführt werden (DIN
EN 1993-1-1, Abs. 6.2.1(6)). |
|
| Nachweisverfahren Elastisch-Elastisch |
 |
Beim Nachweisverfahren Elastisch-Elastisch (E-E) werden
die Schnittgrößen
(Beanspruchungen) auf Grundlage
der Elastizitätstheorie bestimmt.
Der Spannungsnachweis erfolgt mit dem Fließkriterium aus DIN
EN 1993-1-1,
Abs. 6.2.1(5), Formel 6.1. |
|
 |
|
| Nachweisverfahren Elastisch-Plastisch |
 |
Beim Nachweisverfahren Elastisch-Plastisch (E-P) werden die
Schnittgrößen
(Beanspruchungen) auf Grundlage
der Elastizitätstheorie bestimmt. |
Anschließend wird mit Hilfe des Teilschnittgrößenverfahrens
(TSV) mit Umlagerung nach R. Kindmann, J. Frickel: Elastische und plastische Querschnittstragfähigkeit überprüft, ob die Schnittgrößen vom Querschnitt
unter
Ausnutzung der plastischen Reserven aufgenommen werden können
(plastische Querschnittstragfähigkeit). |
| Es können Dreiblechquerschnitte
(I-, C-, U-, Z-, L-, T-Querschnitte) und Rohre als Profile oder typisierte
Querschnitte unter zweiachsiger Beanspruchung einschl.
St. Venant'scher Torsion und Wölbkrafttorsion nachgewiesen werden. |
| Dieses Berechnungsverfahren ist allgemeingültiger als die in
DIN EN 1993 angegebenen Interaktionen für spezielle Schnittgrößenkombinationen. |
| Eine Begrenzung der Grenzbiegemomente wie in DIN 18800, El. 755, ist
in DIN EN 1993 nicht erforderlich. |
|
 |
|
| Die Grenzwerte grenz (c/t) werden je nach Nachweisverfahren aus
DIN EN 1993-1-1, Abs. 5.5.2, Tab. 5.2, ermittelt. |
| Dies entspricht
der Überprüfung der erforderlichen Klassifizierung des
Querschnitts. |
| Läßt die Klassifizierung keinen plastischen
Nachweis zu, wird eine Fehlermeldung ausgegeben. |
|
|
|
 |
|
 |
| Bemessung von Schweißnähten für Biegung und Normalkraft |
|
|
 |
|
Die Spannungsberechnung für Schweißnähte, die durch Biegemomente und Normalkräfte beansprucht werden,
erfolgt gemäß den Regeln der Technischen Biegelehre analog zur Berechnung eines allgemeinen Stahlquerschnitts. |
| Die einzelnen Schweißnahtanteile des Nahtbildes sind gemäß ihrer geometrischen Anordnung alle am Abtrag der Schnittgrößen beteiligt. |
Für die Berechnung der Querschnittswertanteile werden die Nahtflächen als in der Wurzellinie konzentriert
betrachtet (Kehlnähte). |
| Die Querschnittswerte des Nahtbildes ergeben sich durch Summation der Anteile der Einzelnähte. |
|
| Eigenträgheitsmomente von Schweißnähten |
|
|
| Die Eigenträgheitsmomente einer einzelnen Schweißnaht können wie bei einem
schmalen Rechteckquerschnitt berechnet werden. |
|
|
|
| Transformation der Trägheitsmomente bei geneigten Nähten |
|
|
| Da auch senkrechte und geneigte Schweißnähte vorkommen können, muss das Eigenträgheitsmoment
vom lokalen Koordinatensystem in das globale y-z-Koordinatensystem des Stahlquerschnitts
transformiert werden. |
|
|
|
| Die Gesamtfläche Aw der Schweißnähte eines Nahtbildes ergibt sich
als Summe der Flächen der Einzelnähte. |
| Im weiteren Verlauf der Berechnung wird der Schwerpunkt des Nahtbildes berechnet. |
Die Gesamtträgheitsmomente des Nahtbildes können dann aus den transformierten
Einzelträgheitsmomenten
und den Steiner-Anteilen der Einzelnähte aufsummiert
werden. |
|
| Für die Spannungsberechnung werden die Hauptträgheitsmomente und Hauptachsenwinkel des Nahtbildes benötigt. |
| Nach der Transformation der Belastung auf das Hauptachsensystem kann die Spannungsberechnung
erfolgen. |
| Für einen beliebigen Punkt auf einer Schweißnaht lässt sich die Normalspannung
nach der Gleichung berechnen |
|
|
|
| Iη und Iζ sind die Hauptträgheitsmomente
des Nahtbildes; Mη und Mζ sind die auf die
Hauptachsen transformierten Biegemomente. |
Bei umlaufenden Schweißnähten ist der Berechnungsablauf ähnlich
wie zuvor beschrieben. Als zusätzlicher Rechenschritt wird hier die Schweißnaht
automatisch in einzelne Abschnitte aufgeteilt, die als
Einzelnähte
behandelt werden. |
|
 |
| Bemessung von Schweißnähten für Querkräfte |
|
|
 |
|
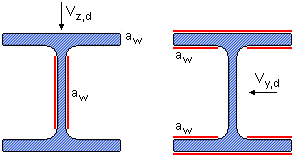
| Gemäß DIN 18800, El. 821, sind beim Spannungsnachweis die Flächen anzusetzen, die aufgrund ihrer Lage vorzugsweise in der Lage sind, die vorhandenen Schnittgrößen in der Verbindung zu übertragen. |
Bei Querkräften sind dies die Nähte, die parallel zur eingetrage-
nen Querkraft verlaufen. |
Bei einem I-förmigen Profil werden die Querkräfte in z-Richtung also von den Stegnähten und die Querkräfte in
y-Richtung von
den Flanschnähten übertragen. |
|
 |
|
|
 |
| Es gibt Schweißnahtbilder,
die nicht zur Übertragung von Querkräften herangezogen
werden können. |
Z.B. sind Flanschnähte
nicht in der Lage, Vz-Lasten
aufzunehmen, weil die Flansche in z-Richtung
eine zu geringe Biegesteifigkeit
aufweisen. |
|
|
|
|
|
|
|
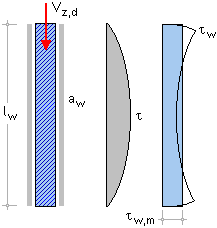
| Die Schubspannungsverteilung in der Schweißnaht weicht von der aus der Biegetheorie
bekannten Parabelform ab. |
Die Schubspannung ist am Nahtende = 0 und erreicht
sehr schnell unweit
des Nahtendes ihren Höchstwert. |
| Diese hohen Schubspannungen
werden durch einen Verzerrungssprung zwischen der steifen Stirnplatte und dem
Schweißnahtende verursacht. |
| Für die Bemessung wird der Schubspannungsverlauf
durch eine konstante Schubspannung angenähert. |
|
|
|
Hierin ist Aw,q der Anteil der Schweißnahtfläche,
der vorzugsweise in der
Lage ist, Querkräfte in z-Richtung zu übertragen. |
|
 |
|
| Für
den gezeigten Rechteckquerschnitt gilt |
|
|
|
 |
| Bemessung von Schweißnähten für Torsionsmomente |
|
|
 |
|
| Die Schweißnahtbemessung für Torsionsmomente kann für Rundrohre und -stähle,
Rechteckrohr- und Rechteckprofile und Flachstähle
mit umlaufender Kehlnaht erfolgen. |
|
|
|
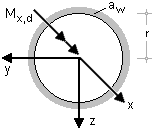
| Die Bemessung der Schweißnähte erfolgt für diese Profiltypen analog der Bemessung
eines dünnwandigen Kreisrings mit der Wandstärke aw. |
| Die Schubspannung, die von einem Torsionsmoment in der Schweißnaht erzeugt
wird, kann berechnet werden mit |
|
|
|
 |
|
| Die Gleichung für das im Nenner stehende Torsionswiderstandsmoment lautet |
|
|
|
| Das Torsionsmoment erzeugt eine konstante umlaufende Schubspannung in
der Schweißnaht, die zu der Schubspannung aus Querkraft
addiert werden muss. |
|
| Rechteckrohre, Rechteckquerschnitte und Flachstähle |
|
|
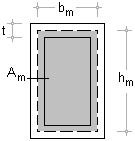
Die Bemessung der Schweißnähte
erfolgt für diese Profiltypen wie die Bemessung
eines dünnwandigen Hohlkastens. |
| Dieses Bemessungsmodell gilt für umlaufende Schweißnähte. |
|
| Hohlkastenquerschnitt: Gemäß der 1. Bredt'schen Formel kann ein Hohlkasten mit der Wandstärke
t mit Hilfe der folgenden Gleichungen bearbeitet werden |
|
|
|
 |
|
|
 |
|
|
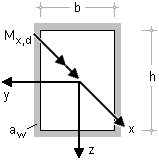
| Rechteckquerschnitt mit umlaufender Kehlnaht: Bei der Berechnung der umlaufenden Schweißnaht
kann analog vorgegangen werden. |
Die Schubspannung in der umlaufenden Kehlnaht eines
rechteckigen Querschnitts
ergibt sich somit zu |
|
|
|
 |
|
|
| Durch das Torsionsmoment wird in der umlaufenden Kehlnaht eine konstante Schubspannung
erzeugt, die zu der Schubspannung aus Querkraft zu addieren ist. |
|
 |
| Bemessung von Schweißnähten bei zusammengesetzter Beanspruchung |
|
|
 |
|
Treten in den Schweißnähten Normalspannungen und Schubspannungen gleichzeitig
auf, sind die Spannungen
zu kombinieren. |
Beim Nachweis des Bauteils selbst
ist der Vergleichsspannungsnachweis zu führen. Für den Nachweis der Schweißnähte
hingegen ist gemäß DIN 18800, El. 825, mit einem Vergleichswert σw,v zu
arbeiten, der
berechnet wird mit |
|
|
| Der Vergleichswert darf nicht mit der aus dem Querschnittsnachweis
bekannten Vergleichsspannung verwechselt werden. Die Vergleichsspannung führt
eine mehraxiale Bauteilbeanspruchung rechnerisch auf eine einaxiale Beanspruchung
zurück. Der
Vergleichswert hingegen ist keine reale Spannung in der Schweißnaht, sondern
ein Versuchswert. |
| Gemäß El. 825 ist nun nachzuweisen, dass der Vergleichswert die Grenzschweißnahtspannung nicht überschreitet |
|
|
|
| Die Grenzschweißnahtspannung ergibt sich gemäß El. 829 zu |
|
|
|
wobei der Abminderungsfaktor αw von der Nahtgüte, der
Stahlgüte
und der Beanspruchungsart abhängig ist;
er kann DIN 18800,Teil
1, Tab.11, entnommen werden. |
|
|
|
 |
|
|
| Die Querschnittsbemessung erfolgt für Lastkombinationen nach Theorie
I. Ordnung (lineare Berechnung) mit dem Verfahren Elastisch-Elastisch. |
| Dazu werden sowohl die Normalspannungen n. Gl. 31, die Schubspannungen n. Gl.
32 als auch die Vergleichs-spannungen n. Gl. 33 nachgewiesen. |
| Örtlich begrenzte
Plastifizierungen n. El. 747, 749 bzw. 750 sind nicht zugelassen. |
|
Die elastischen Normal-, Schub- und Vergleichsspannungen werden in jedem Eckpunkt durch Addition der
Einzelteile
aus den Schnittgrößen berechnet |
|
|
|
| Für die extremalen Spannungen werden die Ausnutzungen berechnet. |
| Die
Spannungsausnutzung ist das Maximum aus den Ausnutzungen der Normal-, Schub-
und Vergleichsspannungsnachweise |
|
|
|
 |
| vereinfachter Beulnachweis |
|
|
 |
|
Stehen einzelne Querschnittsteile unter Druckbeanspruchung, kann ein vereinfachter
Beulnachweis über den
grenz(b/t)-Nachweis geführt werden. |
|
 |
|
| Dazu werden die Druckspannungen eines dünnwandigen Querschnitts nach
Tab. 13, 14 (Verfahren E-E) für den Linienquerschnitt ermittelt. |
Die Ausnutzung
vorh(b/t)/grenz(b/t) wird für alle Linien maximiert, wobei sich unterschiedliche
Werte für
beidseitig
(z.B. Steg, (b/t)o-o) und einseitig gelagerte (z.B. eine
Gurtseite, (b/t)o--) Plattenstreifen ergeben. |
| Die maximale Ausnutzung aus Querschnittsbeulen ergibt sich zu |
|
|
|
|
|
 |
|
|
| Die klassische Stabtheorie geht von der Formerhaltung
des Querschnitts aus. |
Die Querschnittslage lässt sich im lokalen
xyz-Querschnittskoordinatensystem über drei Verschiebungen
ux,
uy, uz und drei Verdrehungen
φx, φy, φz beschreiben. |
Bei der Theorie der Wölbkrafttorsion wird die Verwölbung
des Querschnitts durch das Produkt der
Einheitsverwölbung ω
mit der Verwindung ψx beschrieben. |
|
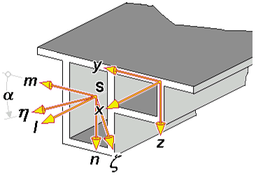
Neben dem xyz-Querschnittskoordinatensystem, in dem
der Quer-
schnitt modelliert wird, gibt es das durch den Schwerpunkt
S
mit
den Koordinaten (ey, ez)
verlaufende lmn-System, dessen Achsen parallel zu den xyz-Achsen verlaufen
(Entkopplung der Fläche und der Trägheitsmomente), und das
durch S verlaufende ξηζ-Hauptachsen-system (Entkopplung
der Trägheitsmomente). |
|
Zur Beschreibung der Torsion wird der
Schubmittelpunkt M mit
den Koordinaten (yM,
zM) als Drehpunkt verwendet (z.B. normierte
Einheitsverwölbung ω, Entkopplung der Biegung und Wölbkraft-
torsion). |
|
 |
|
|
| Die Berechnung der Querschnittswerte und der Spannungen
aus Biegung erfolgt am vollständigen Modell mit Verschneidungen,
Abschrägungen und Ausrundungen. |
Die Verteilung der Schubflüsse,
der Schubspannungen und der Verwölbung längs der Mittellinien
wird am
Linienmodell unter Berücksichtigung der veränderlichen
Dicke ermittelt. |
|
 |
| Schwerpunkt, Trägheitsmomente und Hauptachsen |
|
|
 |
|
| Bei einer konstanten Spannungsverteilung verschwinden
die Biegemomente im Schwerpunkt. |
Die Schwerpunktskoordinaten (ey,
ez) lassen sich mit der Querschnittsfläche
A und den statischen Momenten Sy
bzw. Sz berechen. |
|
|
|
Mit den Trägheitsmomenten im Schwerpunkt lassen
sich im linear elastischen Fall die Schnittgrößen der Biegung
aus der Dehnung εS und den Krümmungen κm, κn ermitteln. |
|
|
|
| Das ξηζ-Hauptachsensystem ist bzgl. des
Querschnittskoordinatensystems um den Winkel α verdreht. |
| Im Hauptachsensystem
ist das Deviationsmoment Imn gleich Null, so
dass die Krümmungen und Momente der Hauptbiegerichtungen entkoppelt
sind. |
|
|
|
Der Hauptachsendrehwinkel ist bis auf ein Vielfaches
von 90° bestimmt. Der Winkel wird so gewählt, dass er bzgl.
des Querschnittskoordinatensystems betragsmäßig möglichst
klein ist. |
|
 |
| Verwölbung und Schubmittelpunkt |
|
|
 |
|
Für dünnwandige Querschnitte berechnet sich
die Wölbordinate ωD,0 für den
Drehpunkt D mit den Koordinaten
(yD, zD)
als Integral des Hebelarms rD der Querschnittspunkte
zum Drehpunkt längs der Profilkoordinate s
(β: Winkel der
Tangente an die Mittellinie). |
|
|
|
| Es wird davon ausgegangen, dass die Verwölbung
in Dickenrichtung konstant ist. |
Die mittlere Querschnittsdehnung der
zugehörigen Einheitsverwölbung ωD ist Null, so dass bei reiner Verwölbung
(im linear elastischen
Fall) keine Normalkraft vorhanden ist. |
|
|
|
| Die Einheitsverwölbungen mit den Drehpunkten (yD,
zD) und (yM, zM)
stehen in folgender Beziehung |
|
|
|
| Der Schubmittelpunkt (yM, zM)
ist der Drehpunkt, für den bei reiner Verwölbung (im linear
elastischen Fall) keine Biegemomente auftreten. Für den Abstand
(ySM, zSM) des Schubmittelpunkts
vom Schwerpunkt ergibt sich |
|
|
|
 |
| Schnittgrößen und Spannungen |
|
|
 |
|
| Die Schnittgrößen ergeben sich durch Integration
der Normal- bzw. Schubspannungen über den Querschnitt. |
Die Schnittkräfte
wirken in Richtung der verformten Querschnittsachsen, die Momente
drehen um die
entsprechenden Achsen in positiver Richtung (Rechte-Hand-Regel). |
|
|
|
Mit den Biegemomenten im Hauptachsensystem, den Torsionsschnittgrößen
um den Schubmittelpunkt und
den entsprechenden Trägheitsmomenten
können im linear elastischen Fall die Normalspannungen aus den
Schnittgrößen ermittelt werden. |
|
|
|
Für dünnwandige Querschnitte werden zur Berechnung des Schubflusses T und der Schubspannung τxs in
Richtung der Profilmittellinien die statischen Momente Sη,
Sζ, Sω und
die Profildicken t in Abhängigkeit der Profilkoordinate s benötigt. |
|
|
|
Tt ist dabei das primäre
Torsionsmoment aus St. Venant'scher Torsion und Tw das sekundäre Torsionsmoment
aus Wölbkrafttorsion. |
| Für Querschnitte mit geschlossenen Zellen kommen noch Schubspannungen
aus den Schubflüssen der einzelnen Zellen hinzu. |
| Die Faktoren
ϑ entsprechen den Einheitsschubflüssen der entsprechenden Schnittgröße. |
| Die Schubspannungen aus Vη, Vζ und Tw bzw. Tt der Zellen
sind nach Voraussetzung konstant in Dickenrichtung. |
| Die Schubspannung
aus Tt der einzelnen Querschnittslinien ist
in Dickenrichtung linear veränderlich und verschwindet auf der
Mittellinie. |
|
|
Neben dem primären Torsionsmoment Tt tritt bei Berechnungen nach Theorie II. Ordnung unter Berücksichtigung
des Wagner-Effekts das Torsionsmoment Tσ infolge Normalspannungen auf. |
|
|
|
| Der Wagner-Koeffizient Kσ lässt sich aus den Schnittgrößen im Hauptachsensystem
berechnen. |
|
|
|
Die Querschnittsstrecken ergeben sich durch Integration
des Quadrats des Schwerpunktabstands rS
über
den Querschnitt. |
|
|
|
|
|
| Die Schubkorrekturfaktoren werden zur Ermittlung der Schubflächen
bzw. Schubsteifigkeiten bei der Berechnung von schubweichen Stäben
benötigt. |
| Die mittlere Schubgleitungen γxy und γxz stehen mit den zugehörigen Querkräften
in Beziehung. |
|
|
|
ϑTy und ϑTz sind dabei die Einheitsschubflüsse der Querkräfte in y- und z-Richtung.
Aus den κ-Werten lassen
sich die Schubkorrekturfaktoren in einem um
den Winkel α verdrehten Koordinatensystem berechnen. |
|
|
|
|
|
| Falls nicht alle Querschnittsteile miteinander verbunden sind,
liegt ein mehrteiliger Querschnitt vor. |
Bei einem derart gespreizten Querschnitt wird
davon ausgegangen, dass die einzelnen Teile durch Riegel oder
Platten so
miteinander gekoppelt sind, dass sie sich affin zueinander verformen. |
| Den Schubmittelpunkt des Gesamtquerschnitts erhält man
durch gewichtete Summation der Schubmittelpunkte der Teile. Die Verwölbung
mit dem Schubmittelpunkt (yM, zM)
als Drehachse des i-ten Teils im Gesamtquerschnitt kann aus der Verwölbung
des Teils mit dem i-ten Schubmittelpunkt (yM,i, zM,i)
als Drehachse berechnet werden. |
Die Verschiebung u in Richtung der Stabachse
bzw. die Längsspannung für den linear-elastischen Fall kann dann
lokal für jedes Teil formuliert werden. |
|
|
|
| Die Querschnittsteile können biegesteif oder biegeschlaff
miteinander verbunden sein. |
| Die Verteilung der Normalkräfte hängt
vom Grad α der Biegekopplung ab (biegesteif: α = 1, biegeschlaff:
α = 0). |
| Der Wert von α hat über den Steiner-Anteil der
Teile Einfluss auf die Trägheitsmomente des Gesamtquerschnitts. |
Die Querschnittswerte des Gesamtquerschnitts erhält man
durch Summation der Querschnittswerte der Teile. |
|
|
|
| Die Normalkräfte verteilen sich im Verhältnis der
Teilflächen. |
|
|
|
| Wenn die Krümmungen der Querschnittsteile identisch sind,
lassen sich die (linear elastischen) Momente Mm,i und
Mn,i der Teile bzgl. ihrer Schwerpunkte aus den Momenten
Mm und Mn des Gesamtquerschnitts
berechnen. |
|
|
|
| Für die Aufteilung der Querkräfte ergeben sich dann
ähnliche Beziehungen. |
|
|
|
Die Torsionsmomente und das Wölbbimoment verteilen sich
im Verhältnis der Querschnittswerte auf
die einzelnen Teile. |
|
|
|
| Die Schnittgrößen des Gesamtquerschnitts erhält
man durch Summation der Teilschnittgrößen. |
|
|
|
|
|
 |
|
 |
| Ergebnisse im y-z-Querschnittskoordinatensystem |
|
|
 |
|
|
|
|
|
|
 |
| Ergebnisse im m-n-Schwerpunktsystem |
|
|
 |
|
|
|
 |
| Ergebnisse im η-ζ-Hauptachsensystem |
|
|
 |
|
|
|
|
|
 |
|
 |
das dritte Register gibt einen Überblick über
die ermittelten Ergebnisse |
|
 |
|
| Zur sofortigen Kontrolle und des besseren Überblicks
halber werden die Ergebnisse in diesem Register lastfallweise übersichtlich
zusammengestellt. |
| Eine Box zeigt an, ob ein Lastfall die Tragfähigkeit
des Anschlusses überschritten hat (rot ausgekreuzt) oder wie viel Reserve noch vorhanden ist (grüner Balken). |
Zur besseren Fehleranalyse oder zur Einschätzung
der Tragkomponenten werden zudem die Einzelberechnungs-
ergebnisse
protokolliert. |
|
| Eine Meldung zeigt an, wenn ein Fehler aufgetreten
oder die Tragfähigkeit überschritten ist. |
| Wenn die
Ursache des Fehlers nicht sofort ersichtlich ist, sollte
die Druckliste in der ausführlichen Ergebnisdarstellung geprüft
werden. |
|
|
|
 |
| zur Hauptseite 4H-EC3SA, SchweißnahtAnschluss |
 |
|
 |
