Seite bearbeitet Juli 2023 Kontakt Programmübersicht Bestelltext Infos auf dieser Seite ... als pdf  undo-Funktion ........................ Skalierungseigenschaften 3D Rechenlaufoptionen ................ Darstellungseigenschaften .... Sichtbarkeitsstatus ............... Detailnachweispunkte ............. Blickrichtung manuell ............. Auswahllisten .......................   Blickwinkelspeicher ................ Systemdruckliste ..................

Die grafische Eingabe eines Platten-/Scheibentragwerks gliedert sich in die fünf logischen Eingabekapitel Modellierung Bildung des statischen Systems Festlegung der Belastung und der zu führenden Nachweise, sowie die Kontroll- und Steuerungsfunktionen

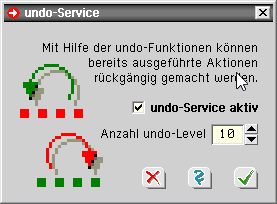
Der nebenstehend dargestellte undo-Button dient dazu, Auswirkungen versehentlich gestarteter Aktionen rückgängig zu machen. Unter Verwendung der Voreinstellung operiert der undo-Mechanismus mit 10 undo-Levels und einem redo- Level. Dies bedeutet, dass die letzten 10 Änderungen am aktuellen Datenzustand sukzessive rückgängig gemacht werden können. Wird die undo-Funktion einmal zu oft aufgerufen, kann mit der redo-Funktion (Wiederherstellen) auch dies bereinigt werden. Die undo/redo-Funktionen speichern den kompletten Datenzustand in temporären undo-Dateien, die nach regulärer Beendigung des grafischen Eingabemoduls gelöscht werden.

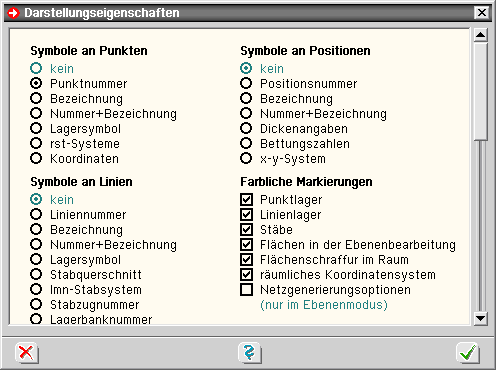
Nach Anklicken des nebenstehend dargestellten Buttons, der sich im rechten Bereich der oberen Buttonzeile befindet, erscheint das Eigenschaftsblatt zur Einstellung der Darstellungseigenschaften der Grafik im Darstellungsfenster. Symbole in der Systemfolie Jedem Objekt (Punkt, Linie, Flächenposition) kann ein Symbol zur Darstellung zugeordnet werden. Welche Symbole bestehen, kann den Auswahllisten entnommen werden. farblich markieren Punktlager, Linienlager und Stäbe können farblich markiert werden. 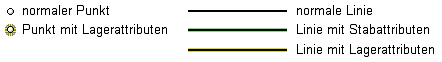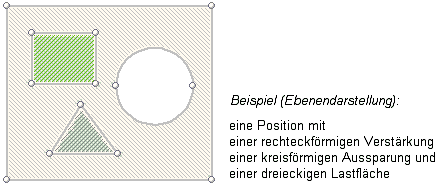Weiterhin kann festgelegt werden, ob Flächen gefüllt werden sollen. In der Ebenenbearbeitung ist es sinnvoll, das Füllen der Flächen auszublenden, wenn eine untergelegte DXF-Folie genutzt werden soll. Im Raum wird die Position durch Schraffurlinien gefüllt, die nach Bedarf ausgeblendet auch werden können. 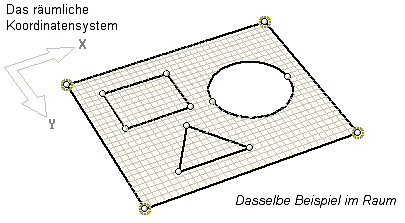Darüber hinaus kann die Darstellung des räumlichen Koordinatensystems im Raum an- bzw. abgeschaltet werden. Lastbilder in der Lastfallfolie Befindet sich die Interaktion in einer Lastfallfolie, werden die hierin definierten Lastbilder dargestellt. Der nachfolgend dargestellten Tabelle kann die Bedeutung der Symbole entnommen werden. In der ersten Spalte ist das Symbol in normaler Form und in der zweiten Spalte im ausgewählten Zustand dargestellt. Die letzte Spalte gibt den zugeordneten, belasteten Objekttyp an. Jeder Lastbildtyp kann von der Darstellung ausgeschlossen und mit oder ohne Ordinatenangabe dargestellt werden. auswählbar sind Nicht nur die Darstellung, sondern auch die Auswählbarkeit der Objekte kann vom Benutzer festgelegt werden. Objekte, deren Auswählbarkeit abgewählt wurde, reagieren nicht mehr auf einen Mausklick. Skalierungen Siehe hierzu Skalierungseigenschaften der Darstellung im 3D.

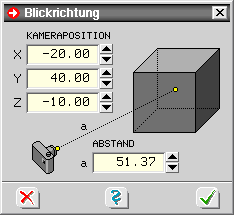
Der nebenstehend dargestellte Button gehört zur Buttongruppe Ansicht und ist nur im 3D-Modus aktivierbar. Wird er angeklickt, kann die Blickrichtung (Kameraposition) numerisch eingestellt werden.

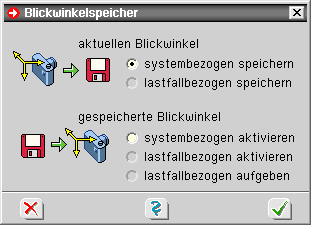
Nach Anklicken des dargestellten Buttons, der sich im rechten Bereich unter der Überschrift Ansicht befindet, erscheint das Eigenschaftsblatt zur Speicherung und Aktivierung der Blickwinkel. Im Blickwinkelspeicher kann die aktuelle Kameraposition system- oder lastfallbezogen gespeichert werden. Ist ein Blickwinkel systembezogen gespeichert, wird dieser Blickwinkel auch bei der Generierung des DTE®-Bauteilsymbols verwendet. Zudem werden die gespeicherten Blickwinkel bei der Erstellung der Grafiken in der Systemdruckliste berücksichtigt.

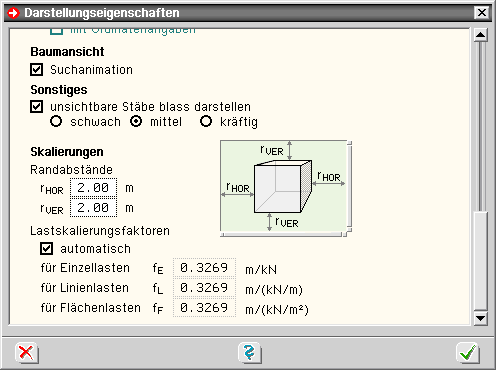
Randabstände Unter Randabstände wird festgelegt, wie viel „Luft" in horizontaler und vertikaler Richtung um die 3D-Konstruktion herum im Objektfenster dargestellt werden soll. Skalierungsfaktoren Für die Einzel-, Linien- und Flächenlasten können Faktoren zur Größenskalierung angegeben werden. Die Voreinstellung für diese Eigenschaft ist automatisch. Hierbei werden die Lastfaktoren für jeden Lastfall unabhängig voneinander programmintern berechnet, indem die größte Ordinate mit 12 % der Raumdiagonalen des umgebenden Quaders des Bauwerks angenommen wird. Der sich hieraus ergebende Skalierungsfaktor wird auf alle Lastordinaten angewandt, jedoch wird eine Mindestgröße bei der Darstellung nicht unterschritten, um die Auswählbarkeit kleiner Einzel- und Linienlasten per Mausklick zu gewährleisten. Die Einstellungen bzgl. der Skalierungsfaktoren werden auch bei der Ausgabe der Lastgrafiken in der Systemdruckliste berücksichtigt.

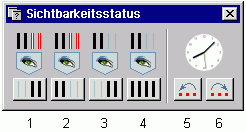
Über den dargestellten Buttons besteht die Möglich-keit, ausgewählte Objekte unsichtbar zu schalten. Hierdurch kann innerhalb von komplexen Strukturen mit sehr vielen Objekten an ausgewählten Detailbereichen gearbeitet werden. Folgende Funktionen stehen zur Verfügung 1. alle Objekte werden unsichtbar geschaltet, die aktuell nicht ausgewählt sind. Es wird mit den aktuell ausgewählten Objekten weitergearbeitet. 2. Es werden alle Objekte unsichtbar geschaltet, die aktuell ausgewählt sind. Es wird mit den aktuell nicht ausgewählten Objekten weitergearbeitet. 3. Sichtbarkeit invertieren: Es werden alle Objekte unsichtbar geschaltet, die aktuell sichtbar sind und umgekehrt. 4. Normalzustand: alle Objekte werden sichtbar geschaltet. 5. definierter Sichtbarkeitsstatus rückwärts: Es wird der Zustand wieder hergestellt, der vor der letzten Änderung des Sichtbarkeitsstatus vorherrschte (Sinnvoll bei sukzessiver Ausschaltung der Sichtbarkeit). 6. definierter Sichtbarkeitsstatus vorwärts: Es wird der Zustand wieder hergestellt, der vor dem letzten Rücksprung vorherrschte. Hierdurch kann zwischen benachbarten Sichtbarkeits-zuständen hin- und hergeschaltet werden.

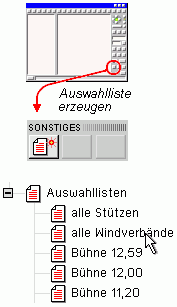
Der aktuelle Auswahlzustand kann in einer Auswahlliste gespeichert werden. Durch Anklicken des markierten Buttons erscheint ein Eigenschaftsblatt, in dem der aktuellen Auswahl eine Bezeichnung zugeordnet werden kann. Diese Auswahl kann durch Anklicken des entsprechenden Symbols im Bauman-sichtsfenster aktiviert werden. Durch Doppelklicken einer definierten Auswahlliste erscheint ein Eigenschaftsblatt, in dem die definierten Auswahllisten eingesehen und verwaltet werden können. Durch Doppelklicken des Wurzelobjekts mit der Bezeichnung Auswahllisten kann in dem hierdurch eingeblendeten Eigenschaftsblatt festgelegt werden, wie das grafische Eingabemodul auf einen Klick auf eine Auswahlliste reagieren soll.

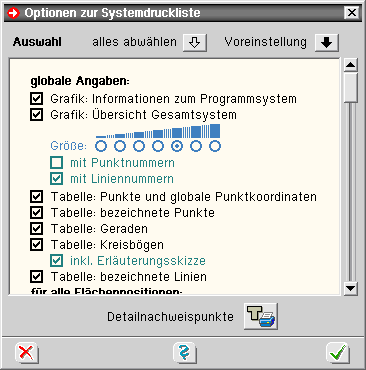
Durch Anklicken des dargestellten Buttons erscheint ein Eigenschaftsblatt auf dem Sichtgerät, in dem die Inhalte der Systemdruckliste festgelegt werden können. Gleichbedeutende Menüfunktion Bearbeiten → Systemdrucklistenoptionen In dem Auswahlfenster können alle Elemente der Systemdruckliste (Grafiken und Tabellen) an- bzw. abgeschaltet werden. Grafiken können hinsichtlich ihrer Größe und ihres Inhalts fein eingestellt werden.

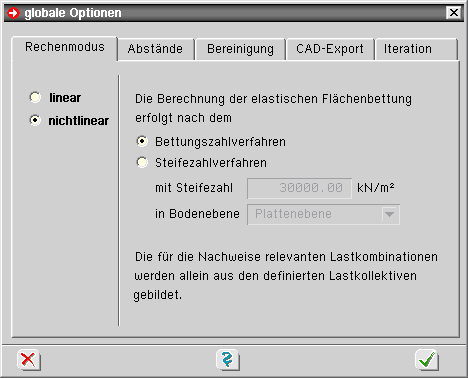
Durch Klicken der nebenstehend dargestellten Buttons können die Angaben zum Rechenmodus eingesehen bzw. geändert werden. Das Eigenschaftsblatt ist in mehrere Register eingeteilt. Register 1: Rechenmodus Der Rechenmodus unterscheidet auf oberster Ebene zunächst zwischen linearem und nichtlinearem Rechenlauf. Beim linearen Rechenlauf werden etwaige elastisch gebettete Flächenpositionen grundsätzlich nach dem Bettungszahlverfahren berücksichtigt. Sind den definierten Nachweisen Extremalbildungsvorschriften und Lastkollektive zugeordnet, werden beide Lastkombinationstypen zur Bildung des extremalen Bemessungswerts herangezogen. Beim nichtlinearen Rechenlauf werden nur die Lastkollektive verwendet, da hier das Super-positionsgesetz keine Gültigkeit besitzt. Die Nichtlinearität besteht grundsätzlich in der Möglichkeit, Zug- bzw. Druckfedern sowohl bei Flächenbettung als auch bei Einzel- und Linienlagern auszuschalten. Bei nichtlinearer Berechnung kann das Verfahren zur Berücksichtigung der elastischen Flächenbettungen gewählt werden. Hier besteht alternativ zum Bettungszahlverfahren das Steifezahlverfahren. Beim Steifezahl-verfahren sind die Bodenebene, die den elastischen Halbraum definiert, und die Steifezahl anzugeben. Alle gebetteten Positionen, die in der angegebenen Ebene liegen, werden nun automatisch nach dem Steifezahlverfahren berücksichtigt. Die der Position zugeordnete Bettungszahl gilt hierbei nur als Startwert der Iteration. nichtlineares Verhalten der Lagerangaben Bei der Definition von Punkt- und Linienlagern sowie bei der Festlegung von elastisch gebetteten Flächenpositionen kann der Anwender Eigenschaften zum nichtlinearen Verhalten festlegen. Diese Eigenschaften werden nur bei der nichtlinearen Berechnung berücksichtigt und geben an, ob die definierte Lagerung immer oder nur bei Verschiebung (des Punkts, der Linie oder der Fläche) in eine bestimmte Richtung wirkt. Hierdurch kann zwischen frei aufliegenden und verankerten Auflagern unterschieden werden. Erfolgt die Berechnung nach dem Steifezahlverfahren und sind elastisch gebettete Positionen in der Bodenebene mit der Festlegung wirkt immer markiert, werden diese Positionen nach dem Bettungszahlverfahren berücksichtigt. 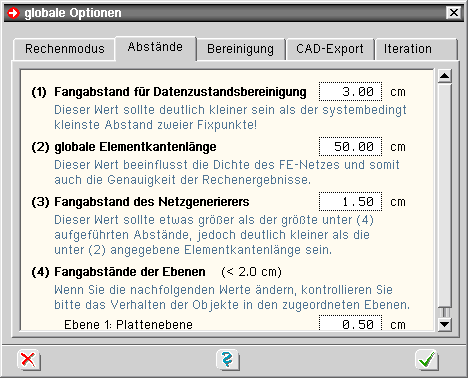Register 2: Abstände Im zweiten Register können vom System in der Interaktion im Eingabemodul als auch im Netzgenerierungsmodul verwendete Abstände festgelegt werden, die an unterschiedlichen Stellen benötigt werden und für die Eingabe des statischen Systems und die fehlerfreie Umsetzung des Systems in ein Finite-Elementnetz maßgeblich sind Fangabstand für Datenzustandsbereinigung Dieser Wert wird bei der automatischen Datenzustandsbereinigung berücksichtigt, die vor der Erzeugung der Eingabedatei für das Rechenmodul durchlaufen wird. Punkte werden bei der Datenzustandsbereinigung vereinigt, wenn ihr räumlicher Abstand zueinander kleiner ist als dieser Fangabstand. Aus diesem Grunde sollte der Wert kleiner sein als der systembedingt kleinste Abstand zweier Fixpunkte. Der eingegebene Wert gilt als Voreinstellung für die manuelle Datenzustandsbereinigung. globale, mittlere Elementkantenlänge Mit diesem Wert wird die Elementdichte für das Gesamtsystem festgelegt und hat maßgeblichen Einfluss auf die Qualität der Ergebnisse. Der Wert wird auch bei der Festlegung der Netzgenerierungsoptionen von Flächenpositionen zur Editierung angeboten. Fangabstand des Netzgenerierers Dieser Wert wird bei der Vernetzung der generierten Knoten vom Netzgenerierungsmodul benötigt und sollte deutlich kleiner sein als die Elementkantenlänge, jedoch etwas größer als der größte Fangabstand der definierten Ebenen. Letztere Bedingung stellt sicher, dass alle in einer Ebene definierten Objekte auch vom Netzgenerierungsmodul als solche erkannt werden. Ist der hier vorgegebene Wert größer als 1/20 der Elementkantenlänge, so wird er auto- matisch vom Netzgenerierer verkleinert. Fangabstände der Ebenen Mit diesen Fangabständen entscheidet das grafische Eingabemodul, welche der insgesamt definierten Objekte Teil der betrachteten Ebene sind. Es empfiehlt sich, bei der Festlegung der Punktkoordinaten möglichst exakt zu arbeiten, um einen zu großen Fangabstand zu vermeiden. 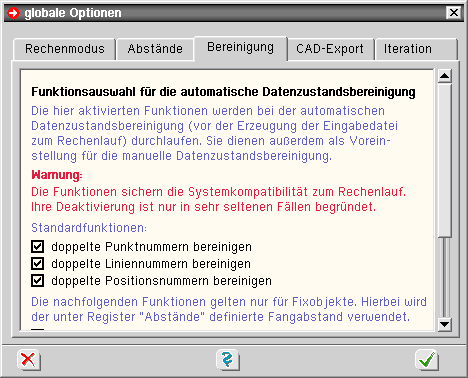Register 3: Bereinigung Im dritten Register kann festgelegt werden, welche Funktionen bei der automatischen Bereinigungsfunktion durchlaufen werden sollen. Da alle hier angebotenen Funktionen den fehlerfreien Ablauf der Berechnung sicherstellen, sollten die Operationen auch teilweise nur in sehr begründeten Fällen deaktiviert werden. 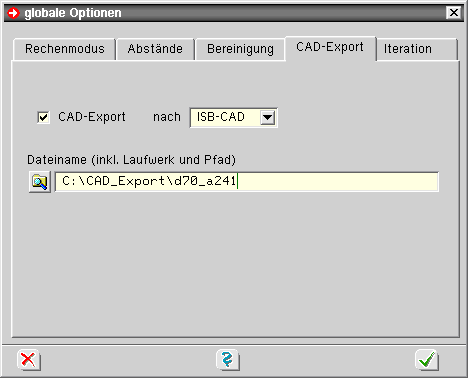Register 4: CAD-Export Im vierten Register kann das Rechenprogramm angewiesen werden, die Informationen bzgl. der erforderlichen Bewehrung über programmspezifische Dateien an ein CAD-System weiterzuleiten. Hierzu existieren Datenformate unterschiedlicher CAD-Hersteller. Für den CAD-Export ist die Eingabe des Namens einer externen Datei erforderlich.

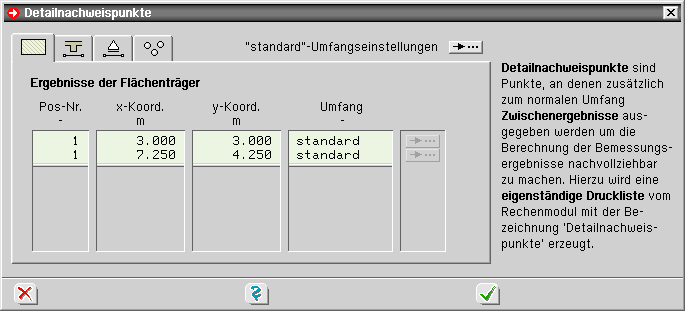
Detailnachweispunkte sind Punkte, an denen zusätzlich zum normalen Umfang Zwischenergebnisse ausgegeben werden, um die Berechnung der Bemessungsergebnisse nachvollziehbar zu machen. Hierzu wird eine eigenständige Druckliste vom Rechenmodul mit der Bezeichnung Detailnachweispunkte erzeugt. Die Eingabe der Detailnachweispunkte erfolgt in den Registern Ergebnisse der Flächenpositionen Ergebnisse der Stäbe Ergebnisse der Lagerlinien Punktergebnisse Der Ergebnisumfang kann für alle Detailnachweispunkte desselben Typs (über die standard-Umfangseinstellungen) oder individuell eingestellt werden.

zur Hauptseite 4H-ALFA, Platte ... 4H-ALFA3D, Faltwerke