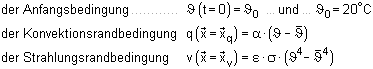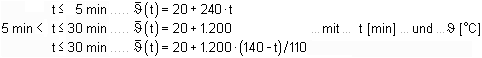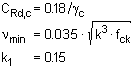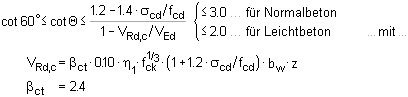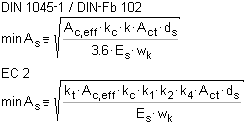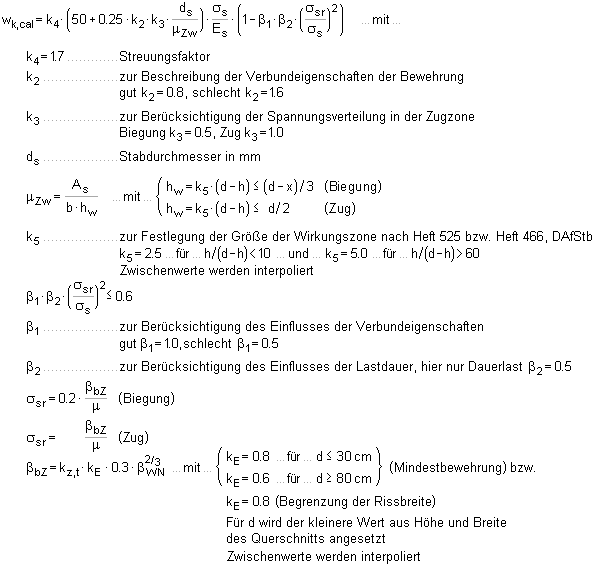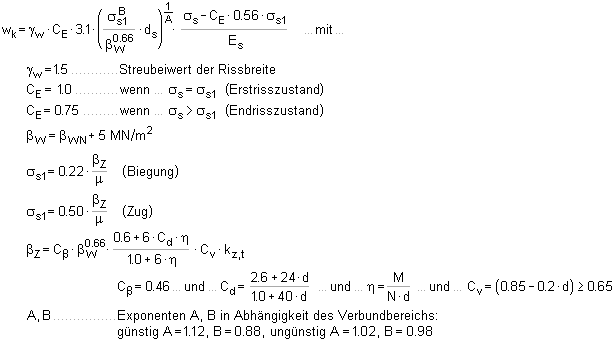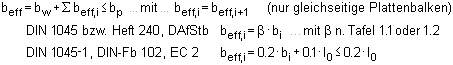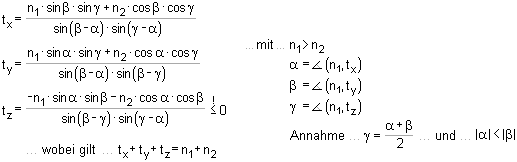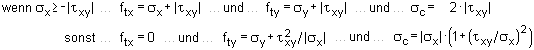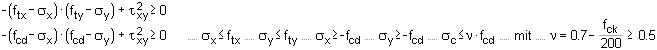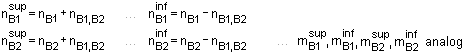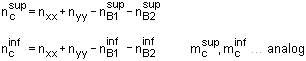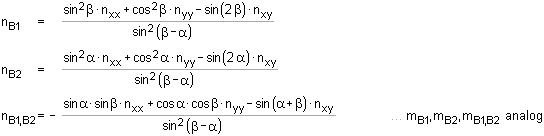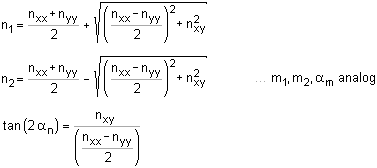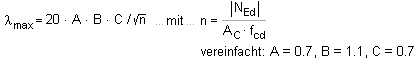|
|
| Seite überarbeitet Juni 2025 |
Handbuch |
.......  |
|
|
Infos auf dieser Seite als pdf |
.......  |
|
|
|
 |
|
Über die folgenden Links erhalten Sie Informationen
zur Stahlbetonbemessung gemäß den o. g. Bemessungs-
richtlinien (Normen), den damit verbundenen Nachweisen und deren Umsetzung
in den 4H-Programmen. |
Die enthaltenen Inhalte sind im Handbuch pcae, Stahlbetontheorie,
abgedruckt.
Das Handbuch kann als pdf-Datei heruntergeladen werden (s.o.). |
| Hier finden Sie Informationen zu |
|
|
| Allgemeines |
 |
|
|
|
| Nachweise im Grenzzustand der Tragfähigkeit |
 |
 |
Schubkraftübertragung in Fugen |
|
|
| Nachweise im Grenzzustand der Gebrauchstauglichkeit |
 |
|
|
|
| Sonderkapitel |
 |
 |
Bemessung von unbewehrtem Beton |
 |
nationaler Anhang zu EN 1992-1-1 und EN 1992-1-2 |
|
|
|
|
|
 |
|
| pcae-Programme unterstützen
- je nach Ausbaustufe - folgende Bemessungsregeln (Normen) |
|
 |
DIN 1045 (7.88) ......................... |
Stahlbetonbemessung |
 |
DIN 1045-1 (7.01) ...................... |
Stahlbetonbemessung im Hochbau |
 |
DIN 1045-1 (8.08) ...................... |
Stahlbetonbemessung im Hochbau |
 |
DIN-Fachbericht 102 (3.09) ......... |
Bemessung von Betonbrücken |
 |
DIN EN 1992-1-1 ....................... |
Eurocode 2: Stahlbetonbemessung im Hochbau |
 |
DIN EN 1992-2 .......................... |
Eurocode 2: Bemessung von Betonbrücken |
|
|
|
| Die Eurocode-nahen Normen DIN 1045-1 und DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
 |
|
| In Auswahlboxen werden die implementierten
Beton- und Betonstahlsorten angeboten. |
|
|
|
|
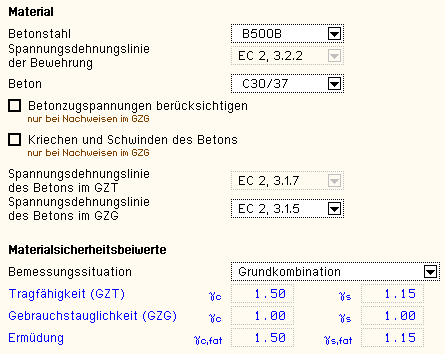 |
| Abb.: Eigenschaftsblatt aus 4H-EC2QB |
|
|
|
|
|
 |
|
| Abb.: Eigenschaftsblätter
aus 4H-EC2QB |
|
 |
|
|
|
|
|
 |
|
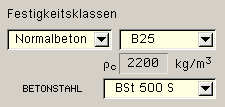
| Nach DIN 1045 dürfen
nur Betone der Festigkeitsklassen |
| B 15, B 25, B 35, B 45, B 55 |
|
| sowie die Betonstahlsorten (nur Stabstahl) |
| BSt 220/340, BSt 420, BSt 500 |
|
| ausgewählt werden. |
|
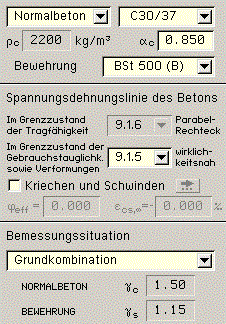
| Nach EC 2 können zusätzlich Betone der Festigkeitsklassen |
C 12/15, C 16/20, C 20/25, C 25/30,
C 30/37, C 35/45, C 40/50, C 50/60, C 55/67,
C 60/75, C 70/85,
C 80/95, C 90/105, C 100/115 |
|
| bzw. die (zugehörigen) Leichtbetone |
LC 12/13, LC 16/18, LC 20/22,
LC 25/28, LC 30/33, LC 35/38, LC 40/44,
LC 50/55, LC 55/60, LC 60/66,
LC 70/77,
LC 80/88 |
|
| sowie die Betonstahlsorten |
| B 500 A, B 500 B, B 550 A, B 550 B, B 600 A, B 600 B (A: normal duktil,
B: hoch duktil) |
| ComBAR GFK, Gitterträger (Sonderstahlgüten) |
|
| ausgewählt werden. |
|
|
|
| es werden nur die in der Norm zugelassenen Beton-
und Stahlsorten unterstützt |
|
|
|
|
| nach 3.1.4 (4) sollten Betonfestigkeitsklassen
über C 50/60 nur verwendet werden, wenn ihr Einsatz hinreichend begründet ist. |
| Nach 3.2.2 (109)P ist für Brückenüberbauten ausschließlich
hoch duktiler Stahl zu verwenden. |
| Leichtbeton darf nicht verwendet werden. |
|
|
|
|
| Tab. 3.1 berücksichtigt Betonfestigkeitsklassen
bis C 90/105. NA-DE lässt auch C 100/115 zu. |
|
|
|
|
| N. NA-DE, Kap. 11, ist Leichtbeton nur mit Zustimmung
der Bauaufsichtsbehörde zugelassen. |
| Sonderstähle werden nicht unterstützt. |
|
|
|
|
|
| Werden Betone der DIN 1045 verwendet, muss
bei einer Bemessung mit Eurocode-nahen Normen die Würfel-druckfestigkeit
in die Zylinderdruckfestigkeit umgerechnet werden (s. Merkblatt
Beton und Betonstahl (DBV 2008)). |
|
| Die Trockenrohdichte des Leichtbetons ist
mit 2.000 kg/m3 > ρ > 800 kg/m3 anzugeben. |
|
| DIN 1045-1 und DIN-Fb
102: Der Abminderungsbeiwert αc zur Berücksichtigung von Langzeitauswirkungen auf
die Druckfestigkeit sowie zur Umrechnung zwischen Zylinderdruckfestigkeit
und einaxialer Druckfestigkeit des Betons ist zu belegen
(i.A. Normalbeton: αc = 0.85, Leichtbeton:
αc = 0.75, EC 2:
αc = 1.0). |
|
| DIN 1045: αc ist bereits in die Betondruckfestigkeit βR bzw. fck eingerechnet. |
|
|
|
|
|
|
 |
|
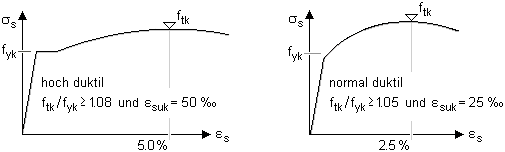
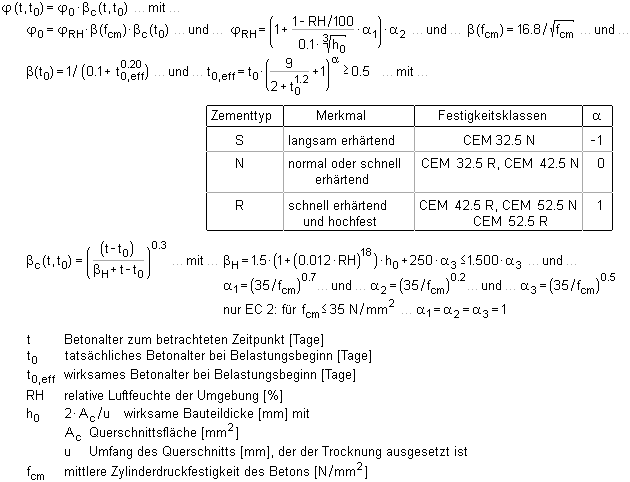
| Die Duktilitätsklassen der Stahlsorten sind folgendermaßen definiert |
|
|
|
| Bei der Bemessung im Grenzzustand der Tragfähigkeit wird stets ein normal duktiler
Betonstahl vorausgesetzt, d.h. |
|
|
| der Verlauf der Spannungsdehnungslinie
von Betonstählen ist n. Bild 12 linear-konstant. |
| Die Bruchdehnung beträgt εsu = 5 ‰. |
|
|
|
|
|
|
|
| benutzerdefinierte Materialien |
|
 |
|
| Die Bezeichnungen der Stahl- und Betongüten
(z.B. B 500 A, C 30/37) stehen für
eine Reihe von Parametern, die zur Berechnung verwendet werden. |
| Auf diese Parameter kann bei benutzerdefinierter
(frei) Materialeingabe direkt
zugegriffen werden (nicht DIN 1045). |
| Dazu sind die benötigten Grenzwerte zur
Beschreibung der Spannungsdehnungslinien anzugeben. |
|
| Beton |
 |
|
|
 |
| Abb.: Eigenschaftsbl. aus 4H-EC2QB |
|
|
|
|
ρc |
Trockenrohdichte in kg/m3 |
|
fck |
charakteristische Zylinderdruckfestigkeit nach 28 Tagen in N/mm2 |
|
εc |
Dehnung bei Erreichen der Festigkeitsgrenze in ‰ |
|
εcu |
Bruchdehnung in ‰ |
|
nc2 |
Exponent der Parabel n. EC 2, 3.1.7, für normalfesten Beton 2.0, für hochfestem
Beton in EC 2, Tab. 3.1,
und für Leichtbeton in EC 2, Tab. 11.3.1, geregelt |
|
fctm |
Mittelwert der zentrischen Zugfestigkeit in N/mm2 |
|
Ecm |
Elastizitätsmodul (Sekantenmodul) in N/mm2 |
|
|
| Bei einer Trockenrohdichte kleiner oder gleich 2000 kg/m³ erfolgt die Bemessung
für Leichtbeton. |
| Die Dehnungen εc1, εcu1 gelten für die wirklichkeitsnahe Spannungsdehnungslinie
(EC 2, Bild 3.2), εc2, εcu2 für das Parabel-Rechteck-Diagramm (EC 2, Bild 3.3)
und εc3, εcu3 für
eine bilineare Beziehung (EC 2, Bild 3.4). |
|
| Bewehrung |
 |
|
|
 |
| Abb.: Eigenschaftsbl. aus 4H-EC2QB |
|
|
|
|
fyk |
| charakteristische Streckgrenze in N/mm2 |
|
| |
ftk |
| charakteristische Zugfestigkeit in N/mm2 |
|
|
εu |
Bruchdehnung in ‰ |
|
Es |
Elastizitätsmodul in N/mm2 |
|
|
|
|
|
|
 |
|
| In einigen Stahlbeton-Bemessungsmodulen
sind spezielle Materialien integriert, die in den Eurocode-nahen
Bemessungsverfahren verwendet werden können. Derzeit
gibt es als "Sonderstahlsorten" |
|
| ComBAR GFK |
 |
|
| Bewehrung aus glasfaserverstärktem
Kunststoff von Schöck Bauteile GmbH (s. www.schoeck.de). |
| Diese Bewehrung ist für besondere
Anforderungen an Korrosionsbeständigkeit, elektrischer
Isolation oder besonderer Resistenz gegen chemischen Angriff entwickelt worden. |
| Die Parameter entsprechen der Zulassung Z-1.6-238 vom 8.7.2019 (Bemessung nach EC 2) |
|
| fyk = ftk = 580 N/mm2,
Es = 60.000 N/mm2, Materialsicherheitsbeiwert
γs = 1.3 |
Die Grenzdehnung ist abhängig von der Betonfestigkeitsklasse
und der statischen Bestimmtheit des Tragwerks.
Es wird der Wert εsu = 0.61 % verwendet. |
|
|
| Gitterträger |
 |
|
| Gitterträger dienen in erster Linie
dazu, nachträglich mit Ortbeton ergänzte Deckenplatten
(Elementdecken) wirtschaftlich und komfortabel herzustellen. |
| Die von den genormten Stahlsorten abweichenden
Materialdaten sind wie folgt definiert |
|
|
|
|
|
| Spannungsdehnungslinien und Sicherheitskonzept |
|
 |
|
| In den nachfolgenden Bildern sind die in den unterschiedlichen
Normen angenommenen Spannungsdehnungslinien und die verschiedenen
Sicherheitskonzepte für Nachweise im Grenzzustand
der Tragfähigkeit in der Übersicht dargestellt. |
|
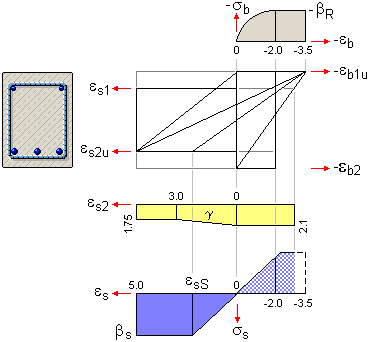
| DIN 1045 |
 |
|
|
| Die Spannungsdehnungsbeziehung
für den Beton (grau unterlegt) wird als Parabel-Rechteck
idealisiert, für den Betonstahl (blau) wird
eine bilineare Spannungsdehnungsbeziehung
angenommen, deren Verlauf nach Erreichen der
Streckgrenze konstant ist. |
| Der Sicherheitsbeiwert (gelb)
variiert in Abhängigkeit der Stahldehnung zwischen 1.75 und 2.1. |
|
| Die Stahlbruchdehnung wird mit εs2u = 5 ‰ |
| und die Betonbruchdehnung mit εb1u = -3.5 ‰ |
| (voll überdrückt εb1 = -2 ‰ angenommen. |
|
| Aus Gründen der Wirtschaftlichkeit (variabler Sicherheitsbeiwert) sollte bei höherer Belastung
die Stahlbruchdehnung nur zu εs2 = 3 ‰ ausgenutzt werden. |
| Bei Bedarf wird programmintern umgeschaltet. |
|
 |
|
|
| Diese Spannungsdehnungslinien werden
auch für die Nachweise im Gebrauchslastzustand mit γ = 1 angesetzt. |
|
| EC 2, DIN 1045-1, DIN-Fb |
 |
|
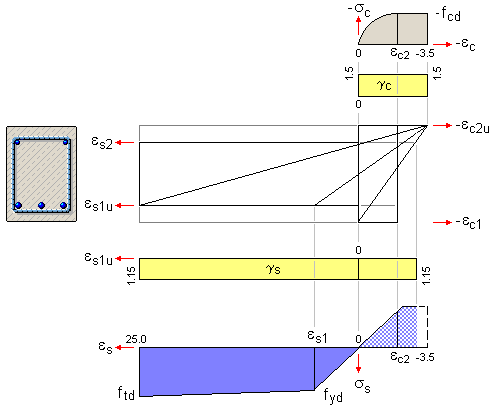 |
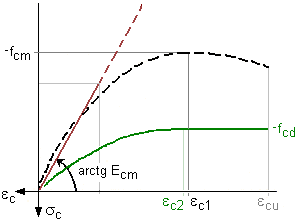
| Die Spannungsdehnungsbeziehung für Nachweise im Grenzzustand
der Tragfähigkeit wird für den Beton (grau unterlegt) nach EC 2, 3.1.7, als Parabel-Rechteck-Diagramm
idealisiert, für den Betonstahl (blau) wird nach EC 2, 3.2.7, eine bilineare Spannungsdehnungsbeziehung
angenommen, die nach Erreichen der Streckgrenze linear veränderlich bis zur Bruchdehnung verläuft. |
| Die Sicherheitsbeiwerte für Beton γc und Stahl γs (gelb)
sind - in Abhängigkeit von der Bemessungssituation - konstant. Sie werden entweder für die
Bemessungssituationen Grundkombination, Erdbeben-Kombination bzw. außergewöhnliche
Kombination vorbelegt oder können vom Benutzer benutzerdefiniert (frei) eingegeben werden. |
| Bei Nachweisen n. EC 2 erfolgt die Vorbelegung durch den eingestellten nationalen Anhang. |
|
| Die Stahlbruchdehnung beträgt εs1u = 25 ‰; die Betonbruchdehnung εc2u (voll überdrückt εc2) ist für EC 2-konforme Betone abhängig von der Güteklasse in EC 2, Tab. 3.1, (Leichtbeton: EC 2, Tab. 11.3.1) angegeben. |
| Aus Gründen der Wirtschaftlichkeit sollte bei höherer Belastung die Druckzonenhöhe
begrenzt werden (s. Vereinfachter Nachweis der plastischen Rotation). |
| Bei Bedarf wird programmintern umgeschaltet. |
|
Für Nachweise im Grenzzustand
der Gebrauchstauglichkeit kann das Materialverhalten des Betons
(Sicherheitsbeiwert γc = 1 bzw.
bei EC 2-Nachweisen der Wert des nationalen Anhangs) wahlweise |
 |
| über das Parabel-Rechteck-Diagramm n. EC 2, 3.1.7, |
|
|
 |
| über die wirklichkeitsnähere Spannungsdehnungsbeziehung n. EC 2, 3.1.5 (empfehlenswert) |
|
|
 |
| oder linear mit αE = Es / Ecm angenommen werden. |
|
|
|
|
| Unterschiede zeigen sich besonders in den Betondruckspannungen, wohingegen die Stahlzugspannungen
nur wenig auf eine Veränderung des Materialverhaltens reagieren. |
|
 |
Bei hoher Belastung (σc > 0.4·fcm)
erweist sich das Parabel-Rechteck-Diagramm n. EC 2, 3.1.7, als zu
‚weich', während der lineare Ansatz zu hohe Werte liefert. |
Die realitätsnahe Abbildung der Spannungsdehnungsbeziehung des Betons
n. EC 2, 3.1.5, berücksichtigt
in den geringen Dehnungsbereichen das lineare Materialverhalten
und bei hoher Belastung den sanften Übergang zur Bruchspannung. |
|
|
|
|
Als Spannungsdehnungslinie des Betonstahls wird analog
EC 2, 3.2.7, ein bilinearer Verlauf
mit γs = 1 angenommen,
dessen Dehngrenze mit der Duktilitätsklasse variiert. |
|
 |
|
|
|
|
|
| vereinfachter Nachweis der plastischen Rotation |
|
 |
|
| Nach EC 2, 5.6.3, wird programmintern berücksichtigt für |
|
|
|
|
|
|
| Bei Bedarf kann für Balken
der Grenzwert lim kx variiert werden (nur 4H-EC2QB). |
| Die Einhaltung der Druckzonenhöhe erfolgt jedoch nur, wenn |
|
| d.h. wenn in Stahlfaser 2 εyd ausgenutzt wird. |
| Falls kein Gleichgewichtszustand gefunden wird, wird programmintern auf einlagige Bewehrungsanordnung umgeschaltet. |
|
|
|
|
|
 |
|
| Nachweise, die im Grenzzustand der Gebrauchstauglichkeit geführt werden, beziehen
sich häufig auf einen Zeitpunkt (Endzeitpunkt der Nutzbarkeit, i.A. 70 Jahre),
an dem das Betonkriechen und -schwinden nicht vernachlässigbar ist. |
Diese Einflüsse können über eine Modifikation der Spannungsdehnungslinie des Betons
berücksichtigt
werden (nicht DIN 1045). |
|
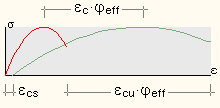
|
| Vergrößerung der Dehnungen εc, εcu sowie |
| Verringerung des E-Moduls Ecm um den Faktor (1 + φeff) |
|
|
|
| Verschiebung der Spannungsdehnungslinie um das Maß εcs |
|
|
|
| Grafik: Der Einfluss der Kriechens und Schwindens
ist anhand der wirklichkeitsnahen Spannungsdehnungslinie
für Beton dargestellt (rote Linie: ohne, grüne Linie: mit Einfluss). |
|
|
 |
|
|
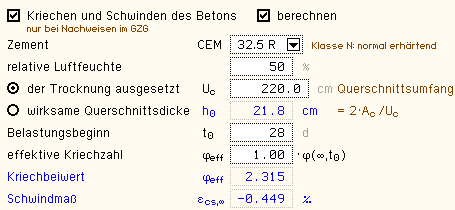
Die effektive Kriechzahl φeff und das Schwindmaß εcs können entweder
vom
Anwender direkt vorgegeben oder vom Programm n. EC 2, 3.1.4, bzw. Heft 525, DAfStb, berechnet werden. |
|
| Abb.: Eigenschaftsbl. aus 4H-EC2QB |
|
 |
|
|
| Der Dauerlastfaktor kann abgeschätzt werden zu |
|
| Berechnung der Endkriechzahl φ (∞, t0) zum Zeitpunkt t = ∞ = 70 Jahre |
|
|
| Voraussetzung: konstante Spannung, d.h. Betondruckspannung zum Zeitpunkt
t0 nicht größer als 0.45 · fck |
| Kriechzahl zum Zeitpunkt t |
|
|
| Berechnung der Schwinddehnung εcs zum Zeitpunkt t = ∞ = 70 Jahre |
|
| EC 2 Schwindverformung zum Zeitpunkt t |
|
|
|
| DIN 1045-1, Fb 102 n. Heft 525, DAfStb Schwindverformung zum Zeitpunkt t |
|
|
|
|
|
|
|
|
 |
|
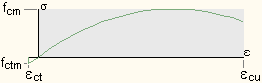
| Bei der Dehnungs- und Spannungsermittlung
im Grenzzustand der Gebrauchstauglichkeit können Betonzugspannungen
berücksichtigt werden. |
| Es wird der Ansatz verfolgt, dass die
Betonzugspannungen sich linear verhalten bis zum Zugbruch bei εct = fctm / Ecm. |
| Da die Betonzugfestigkeit i.A. sehr klein ist gegenüber der Druckfestigkeit, ist der Einfluss
auf das Berechnungsergebnis gering. |
|
 |
|
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| Anforderungen an die Bewehrungsanordnung |
|
 |
|
| DIN 1045, 17.2 |
Nach 25.2.2.1 ist bei Druckgliedern ein
minimaler Bewehrungsgrad von 0.8% des statisch erforderlichen
Querschnitts zu berücksichtigen. Im Programm kann dieser Mindestbewehrungsgrad
frei eingestellt werden. |
|
| DIN 1045-1, 10.2 / DIN-Fb 102, 4.3.1 |
Zur Sicherstellung eines duktilen Bauteilverhaltens
ist bei überwiegend biegebeanspruchten Bauteilen nach
13.1.1(1) eine Mindestbewehrung (Robustheitsbewehrung)
vorzusehen. Hierzu wird bei der Extremierung ein zusätzlicher
Lastfall für das Rissmoment Mcr = fctm·Wc angesetzt und mit fyk bemessen. |
|
| Die Mindestbewehrung für Stützen (stabförmige
Druckglieder) beträgt nach 13.5.2(1) |
|
|
| Abweichend von DIN 1045-1 muss nach DIN-Fb
102, 5.4.1.2.1(1)*P außerdem eingehalten
werden |
|
|
| Für Wände ist Abschnitt 13.7.1(3) zu berücksichtigen,
in dem gefordert wird, dass die lotrechte Bewehrung |
|
|
| nicht unterschreitet. |
Allerdings darf nach DIN 1045-1 (8.08) die Mindestbewehrung auch belastungsabhängig wie
für Stützen
ermittelt werden |
|
|
|
| EC 2, 6.1 |
| Zur Vermeidung schlagartigen Versagens ist
bei überwiegend biegebeanspruchten Bauteilen nach 9.2.1.1(1)
eine Mindestbewehrung vorzusehen. |
|
|
| Die Mindestbewehrung für Stützen (stabförmige
Druckglieder) beträgt nach 9.5.2(2) |
|
|
| Für Wände ist Abschnitt 9.6.2(1) zu berücksichtigen,
in dem gefordert wird, dass die vertikale Bewehrung |
|
| nicht unterschreitet. |
|
|
|
|
|
|
 |
|
| In Abhängigkeit der jeweiligen Schnittgrößenkombination
werden Zug- und Druckrand bestimmt sowie die vorgegebene Bewehrungsanordnung
überprüft. |
Lässt sich kein eindeutiger Zug-/Druckrand definieren
(zentrisch belasteter Querschnitt mit einer bezogenen
Ausmitte
Druck: e/d < 0.35, Zug: e/d < 0.20 mit e = |M/N|),
muss die Bewehrung oben und unten symmetrisch eingelegt werden. |
Soll ein unbewehrter Querschnitt bemessen werden, kann lediglich die
bezogene Tragfähigkeit (Sicherheitsnachweis)
des Betonquerschnitts ermittelt werden. |
|
| Für jeden Lastfall wird unter Berücksichtigung
des minimalen (Mindestbewehrung s.o.) und maximalen Bewehrungsgrades
die erforderliche Längsbewehrung bestimmt. |
Werden sämtliche Lastfälle fehlerfrei bemessen,
ergeben sich die maximal erforderlichen Bewehrungsquerschnitte
oben und unten zu erf Aso und erf Asu.
Da nach DIN 1045 der Sicherheitsbeiwert γ variabel ist,
wird dieser stets protokolliert. |
|
Außerdem werden die Bruchdehnungen εb1u,
εs2u, εb2u (DIN 1045)
bzw. εc2u, εs1u, εc1u (DIN 1045-1) sowie die Hilfsbeiwerte für die Höhe der Druckzone
kx = εb1 / (εb1 - εs2)
= x / hstat, den inneren Hebelarm kz =
z / hstat, die
statische Höhe hstat und
(bei Kreisquerschnitten) die effektive Breite bw angegeben. |
|
Ergibt die Extremierung der Bewehrungsquerschnitte
unter Berücksichtigung einer benutzerdefinierten
Grundbewehrung As0o bzw. As0u eine Überschreitung des
maximal zulässigen Bewehrungsgrades, erfolgt
im Ergebnisausdruck ein entsprechender Hinweis. |
|
|
|
|
|
|
 |
|
Besteht die Längsbewehrung
aus glasfaserverstärktem Kunststoff, wird der
maximale Bewehrungsgrad mit
max ρ = 3.5% angesetzt. |
| Eine Druckbewehrung darf nicht verwendet
werden. |
|
|
|
|
|
 |
|
| Die Querschnittsausnutzung wird für den schlussendlich
erforderlichen Bewehrungsquerschnitt über den Sicherheitsnachweis
ermittelt (U = 1/t). |
| Die zugrunde liegenden Schnittgrößenkombinationen
resultieren aus dem Grenzzustand der Tragfähigkeit (Biegebemessung). |
| Für vorwiegend auf Druck beanspruchte Querschnitte
wird überprüft, ob die Bewehrung für einen Brandschutznachweis
(Einteilung in Feuerwiderstandsklassen nach DIN 4102-4) ausreicht. |
| Dazu muss nach DIN 4102-22 der Ausnutzungsfaktor |
|
|
|
| als Eingangswert in die Tabellen ermittelt werden. |
|
| Ist α1 > zul α1,
wird die Bewehrung so lange iterativ erhöht (SRd vergrößert), bis α1 = zul α1 ist. |
Mit diesem α1-Wert wird dann
für Stützen nach Tab. 31, für Wände nach
Tab. 35 (1-seitige Brandbeanspruchung), DIN 4102-4 die Feuerwiderstandsklasse ausgegeben. |
|
| Im umgekehrten Fall kann die Einhaltung einer
bestimmten Feuerwiderstandsklasse u.a. über zul α1 gesteuert werden. |
|
Nach neuen Erkenntnissen (s. Technische Regeln
zum Brandschutz, BK 2007 T.2 bzw. Fingerloos/Richter)
kann bei der Stützenbemessung auf den Faktor α* verzichtet
werden, wenn die geänderte Tab. 31 zur
Benennung der Feuerwiderstandsklasse herangezogen wird. |
| Wird der Faktor α* zu Null gesetzt, muss
die Stützenlänge im Brandfall lcol vorgegeben
werden. |
| Der maximal zulässige Ausnutzungsfaktor darf
dann zul α1 = 0.7 nicht übersteigen. |
|
| Kann die Tabelle nicht angewandt werden, wird
eine Fehlermeldung ausgegeben. |
|
|
 |
DIN 4102-4: Brandverhalten von Baustoffen und
Bauteilen – Teil 4: Zusammenstellung und Anwendung
klassifizierter Baustoffe, Bauteile und Sonderbauteile, Ausgabe März 1994 |
|
 |
| DIN 4102-4/A1: Brandverhalten von Baustoffen und Bauteilen
– Teil 4: Zusammenstellung und Anwendung klassifizierter Baustoffe,
Bauteile und Sonderbauteile, Änderung A1, Ausgabe November 2004 |
|
 |
| DIN 4102-22: Brandverhalten von Baustoffen und Bauteilen –
Teil 22: Anwendungsnorm zu 4102-4 auf der Bemessungsbasis von
Teilsicherheitsbeiwerten, Ausgabe November 2004 |
|
 |
H.M. Bock, E. Klement: Brandschutz-Praxis für Architekten
und Ingenieure, 2. Auflage,
Bauwerk-Verlag GmbH, 2006 |
|
 |
N.A. Fouad, A. Schwedler: Brandschutz-Bemessung auf einen
Blick nach DIN 4102,
Bauwerk-Verlag GmbH, 2006 |
|
 |
Musterliste der Techn. Baubestimmungen, Kap.3 Technische Regeln
zum Brandschutz,
Betonkalender 2007, Teil 2 |
|
 |
| F. Fingerloos, E. Richter: Zur Heißbemessung von Stahlbetonstützen,
Der Prüfingenieur, April 2007 |
|
|
|
|
 |
|
| Nach EC 2 ist es gegenwärtig möglich,
ein Verfahren zur Bestimmung einer adäquaten Leistungsfähigkeit
eines brandbeanspruchten Bauteils (Standhalten gegenüber einer Brandeinwirkung)
durchzuführen. |
| In pcae-Programmen sind zwei Verfahren
anwendbar |
 |
ein vereinfachtes Rechenverfahren nach
4.2 (Zonenmethode nach Anhang B.2) |
|
 |
ein vereinfachtes allgemeines Rechenverfahren in Anlehnung an 4.3 |
|
|
| Beide Verfahren basieren auf einer thermischen
Analyse des Bauteils unter Berücksichtigung thermischer
Einwirkungen und temperaturabhängiger Materialeigenschaften. |
| Die Temperaturprofile in einem Stahlbetonbauteil
werden ohne Mitwirkung der Bewehrung ermittelt. |
| Die mechanische Analyse baut auf den temperaturabhängigen
Veränderungen der mechanischen Materialeigenschaften –
auch der thermisch bedingten Dehnungen und Spannungen (Eigenspannungszustände)
– auf. |
| Die Einwirkungskombination infolge Brandbeanspruchung
ist ‚außergewöhnlich’ und wird mit charakteristischen
Materialkennwerten γc = γs = 1 bemessen. Kriechen und Schwinden sind unmaßgeblich. |
|
| In pcae-Programm können folgende
Querschnitte brandbemessen werden |
 |
| 2-achsige Bemessung: ein willkürlich, d.h.
von oben, unten, links, rechts beflammter Rechteckquerschnitt |
|
 |
1-achsige Bemessung: ein
von oben, unten, seitlich beflammter Rechteckquerschnitt, ein von oben, unten
beflammter Plattenbalken und Doppel-T-Querschnitt sowie ein
von allen Seiten
gleichmäßig beflammter Kreisquerschnitt |
|
|
|
|
|
|
| Die instationäre Wärmetransportgleichung
ist eine partielle Differentialgleichung 2. Ordnung 1. Grades.
Sie gehört zur Kategorie der parabolischen Differentialgleichungen. |
|
| Es handelt sich um ein Anfangs-Randwertproblem ohne Wärmequellen (φ = 0) mit |
|
| Über Konvektion und Strahlung wird eine zeitlich
veränderliche Brandkurve eingesteuert. |
| In den pcae-Programmen sind aktuell vier Brandkurven implementiert. |
| Die Einheits-Temperaturzeitkurve (EC 1-1-2, Kap.
3.2.1) ist n. NA-DE i.d.R. im Hochbau anzuwenden. |
| Sie wird berechnet mit |
|
| Zum Nachweis des Raumabschlusses bei nicht tragenden
Außenwänden, Brüstungen und für Fassadenteile
darf als Brandbeanspruchung von außen die Außenbrandkurve
n. EC 1-1-2, Kap. 3.2.2 verwendet werden. |
| Sie wird berechnet mit |
|
| Die Hydrokarbon-Brandkurve
n. EC 1-1-2, Kap. 3.2.3 wird für Brände angesetzt, die durch
Flüssigkeiten z.B. in Industrieanlagen verursacht werden. |
| Sie ist n. NA-DE für Hochbauten mit üblichen Mischbrandlasten nicht zu verwenden;
sie wird berechnet mit |
|
| Als Sonderfall wird die ZTV-ING-Brandkurve für
Tunnelanlagen angeboten (s. Bundesministerium
für Digitales und Verkehr: Zusätzliche Vertragsbedingungen
und Richtlinien für Ingenieurbauten, ZTV-ING, 2025). |
| Sie wird berechnet mit |
|
|
| Die allgemeine Lösung kann nur mit Hilfe
von Näherungsverfahren ermittelt werden. |
In pcae-Programmen kommt eine semidiskrete
Finite-Volumen-Formulierung (FVM) zur Anwendung, d.h.
die Ortsdiskretisierung
erfolgt durch die finite Volumenmethode, während in Zeitrichtung
ein explizites
Differenzenverfahren angewandt wird. |
| Vorteilhaft an FVM ist die lokale Konservativität
(hier: Temperatur- bzw. Energieerhaltung) um jeden Zellknoten
herum, da die Differentialgleichung in jedem Kontrollvolumen
erfüllt sein muss. |
|
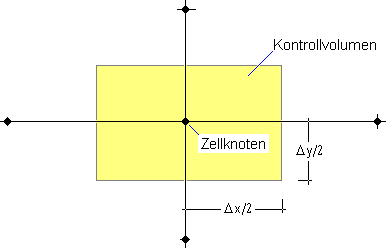
| Zunächst wird der Querschnitt diskretisiert;
es wird ein rechteckiges Gitter zu Grunde gelegt. Für jeden
Gitterknoten (Zellknoten) wird ein Kontrollvolumen definiert,
über dem die Differentialgleichung integriert wird. |
|
| Beispiel einer Kreisdiskretisierung (Ausschnitt) |
|
| Je feiner der Querschnitt durch finite
Volumen aufgelöst wird, desto glatter können
die Isolinien der Temperatur ermittelt werden. |
| Diese Genauigkeit ist allerdings in
den meisten Fällen nicht erforderlich. |
|
 |
|
|
| Es ist üblich, das Kontrollvolumen aus den
Vertikalen der Mittelpunkte der Zellkanten zu bilden. |
Die Zeitdiskretisierung erfolgt explizit mit konstanten Zeitschritten, daher ist als
Stabilitätsbedingung das
Neumann-Kriterium einzuhalten |
|
| Der Zeitschritt wird automatisch an die Gegebenheiten angepasst. |
| Die temperaturabhängigen Materialparameter |
 |
| λ Wärmeleitfähigkeit [W/m K] |
|
 |
| c spezifische Wärme [kJ/kg K] |
|
 |
|
|
|
| werden nach EC 2 bestimmt und iterativ im Programm berücksichtigt. |
| Folgende Parameter sind festzulegen |
|
 |
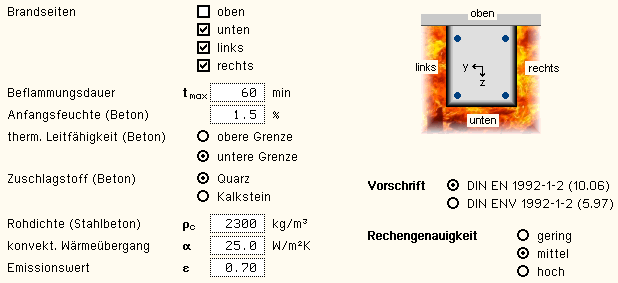
| die Brandseiten eines Rechteckquerschnitts beziehen
sich auf das lokale Koordinatensystem (siehe Grafik). Bei zweiachsiger
Bemessung kann willkürlich gewählt werden. |
|
 |
die Beflammungsdauer steuert die zu erstrebenden Feuerwiderstandsklasse.
R 90 entspricht z.B. einer
Branddauer von tmax = 90 min. |
|
 |
| die Anfangsfeuchte des Betons hemmt die Ausbreitungsgeschwindigkeit
der hohen Temperaturen. Sie geht in die Ermittlung der spezifischen
Wärme ein. |
|
 |
| im EC 2 werden zwei Kurven zur Bestimmung der thermischen
Leitfähigkeit des Betons angeboten, die im Programm frei
wählbar sind. Nach Anhang A (2) ergibt der untere Grenzwert
realistischere Betontemperaturen als der obere. |
|
 |
| der Zuschlagstoff des Betons beeinflusst das Querschnittsverhalten
und ist daher stets mit anzugeben. |
|
 |
| die Rohdichte von Stahlbeton enthält auch den Anteil
der Bewehrung und ist daher stets gleich oder größer
als die Dichte des Betons. |
|
 |
die Temperatur wird über Konvektion und Strahlung in
den Querschnitt eingeleitet. Hierzu sind die entspr.
Parameter des konvektiven Wärmeübergangs und der Emissionswert
einzugeben. Werden sowohl α als
auch ε mit Null
belegt, wird die Temperatur als Dirichlet'sche (direkte) Randbedingung
aufgebracht. |
|
 |
| es besteht die Möglichkeit, die Stoffparameter auch nach
der Vornorm des EC 2 (DIN ENV 1992-1-2 (5.97)) berechnen zu
lassen. |
|
 |
| die Berechnung des Temperaturprofils kann - besonders bei
kleinen Querschnitt und hohen Branddauern - viel Zeit benötigen,
da der Zeitschritt von der Größe des Kontrollvolumens
abhängt. Daher besteht die Möglichkeit, die Rechengenauigkeit
zu beeinflussen. |
|
|
|
|
|
|
| Mechanische Analyse - Bemessungsverfahren |
|
|
| Die Brandursache führt zu einer
nichtlinearen Änderung der Materialkennwerte über den Querschnitt. |
| Allgemeine Bemessungsverfahren definieren daher im Querschnitt
mehrere Betonbereiche, jeder mit etwa gleicher mittlerer Temperatur
(gleichen Materialwerten), und erfassen dadurch die tragwirksamen Bereiche zuverlässig. |
| Der kalte innere Bereich und die heiße Randzone wirken beim Lastabtrag nicht mit. |
Basierend darauf wurden Näherungsverfahren entwickelt,
die den ingenieurmäßigen Anforderungen
Rechnung tragen. |
| Der Betonquerschnitt wird dabei mit einer gleichmäßigen
Temperaturerhöhung beaufschlagt, die das wirkliche Tragverhalten
bestmöglich wiedergibt. |
| Die Temperatur in der Bewehrung kann genau genug im Zentrum
des Bewehrungsstahls angenommen werden. |
|
| Das Zonenverfahren basiert auf der
Annahme einer beidseitig beflammten Modellwand. |
| Der Querschnitt wird in eine vorgegebene
Anzahl von n Zonen gleicher Breite eingeteilt. |
| Im zentralen Horizontalschnitt wird für
jede Zone i die Mittentemperatur ϑc,i und daraus der Reduktionsbeiwert kc,i ermittelt. |
| Über |
|
 |
|
|
| kann dann eine mittlere Betontemperatur berechnet werden, die gleichmäßig in dem um |
|
| reduzierten Querschnitt gilt. |
Die Breite w entspricht
der halben Modellwandbreite, kc(ϑm) ist der Reduktionskoeffizient für
Beton in der
Mittelachse der Modellwand. |
| Die Bemessung erfolgt im Grenzzustand der Tragfähigkeit. |
|
 |
| Mit dem Zonenverfahren können
derzeit nur Rechteck- oder Kreisquerschnitte bemessen
werden. |
|
|
|
|
|
| In pcae-Programmen wird
die Betontemperatur je Zone über deren Breite gemittelt. |
| Daher kann der Korrekturfaktor (1 - 0.2/n)
zur Berechnung des mittleren Reduktionsfaktors kcm entfallen. |
Zudem besteht die Möglichkeit,
den az-Wert vorzugeben (z.B. nach EC 2, Anhang B.2,
Bild B.5, oder Vornorm
des EC 2 (ENV), Anhang B, Bild B.3). |
| Zur Bemessung wird die über den
reduzierten Querschnitt integrierte, mittlere Betontemperatur herangezogen. |
| Optional kann auch die Temperatur des kältesten
Querschnittspunkts (Mittelpunkt) herangezogen werden. |
Für diese Temperatur wird über
den Beiwert kc die charakteristische Druckfestigkeit
unter
Hochtemperaturbelastung bestimmt. |
| Die Temperatur der Bewehrung kann
genügend genau im Schwerpunkt des Betonstahls angenommen
werden. Sie beeinflusst den Abfall der charakteristischen Zug-
und Druckfestigkeit fyk der Bewehrung. |
| Näherungsweise und auf der sicheren
Seite liegend wird der Abminderungsbeiwert ks der
Bewehrung immer für gedrückten Stahl angesetzt. |
Die Form der Spannungsdehnungslinien
kann entweder analog der Kaltbemessung oder nach EC 2 (Brandfall,
Kap. 3.2 bzw. ENV, Anhang A) gewählt werden. |
| Um die inneren Spannungen aus Temperatur
zu berücksichtigen, werden die Spannungsdehnungslinien
in Abhängigkeit ihrer Temperatur vorgestaucht, d.h. die
Spannungsdehnungslinien werden um den Wert εV,
θ verschoben. |
|
Cyllok/Achenbach (s. Literatur)
nehmen für die Bemessungstemperatur des Betons die Temperatur
im
Mittelpunkt des Querschnitts θM ≥ 100 °C an. |
| Die Form der Spannungsdehnungslinien
entspricht dem EC 2 (Brandfall), wobei die Spannungsdehnungslinie der Bewehrung auf der Druckseite
eine Druckspannungsreduktion von Δϑ = 0.2% · Es,ϑ erfährt. |
|
| Das vereinfachte
allgemeine Rechenverfahren bietet eine Möglichkeit,
auch allgemeine Querschnittsformen brandschutztechnisch zu beurteilen.
Wie zuvor besteht das Problem in der Bestimmung der mittleren
Betontemperatur und der geschädigten Randzone. |
|
 |
|
|
| Die geschädigte Randzone sei
der Bereich des Querschnitts, in dem die Temperatur einen kritischen
Wert übersteigt. |
| Sie kann vom Benutzer vorgegeben werden; pcae empfiehlt Θcrit = 500 °C. |
| Die Betontemperatur wird wie beim
Zonenverfahren über den reduzierten Querschnitt aufintegriert.
Ebenso können die Spannungsdehnungslinien nach der Kaltbemessung
oder EC 2 (Brandfall) angenommen werden. |
|
| Die Bemessung erfolgt im Grenzzustand der Tragfähigkeit. |
|
Bei hochfestem Beton (von
C55/67 bis C90/105) wird eine Reduzierung der Festigkeit nach EC 2,
Tab. 6.1N, vorgenommen. |
Der unwirksame Querschnittsbereich
ermittelt sich nach dem vereinfachten allgemeinen Rechenverfahren zu
az = k·a500, mit k aus dem Nationalen Anwendungsdokument. |
Der empfohlene Wert ist 1.1 für
Klasse 1 und 1.3 für Klasse 2. Die empfohlene Klasse für
Beton C55/67
und C60/75 ist Klasse 1, für Beton C 70/85
und C 80/90 ist Klasse 2 und für Beton C 90/105 ist Klasse 3. |
|
|
|
|
|
 |
|
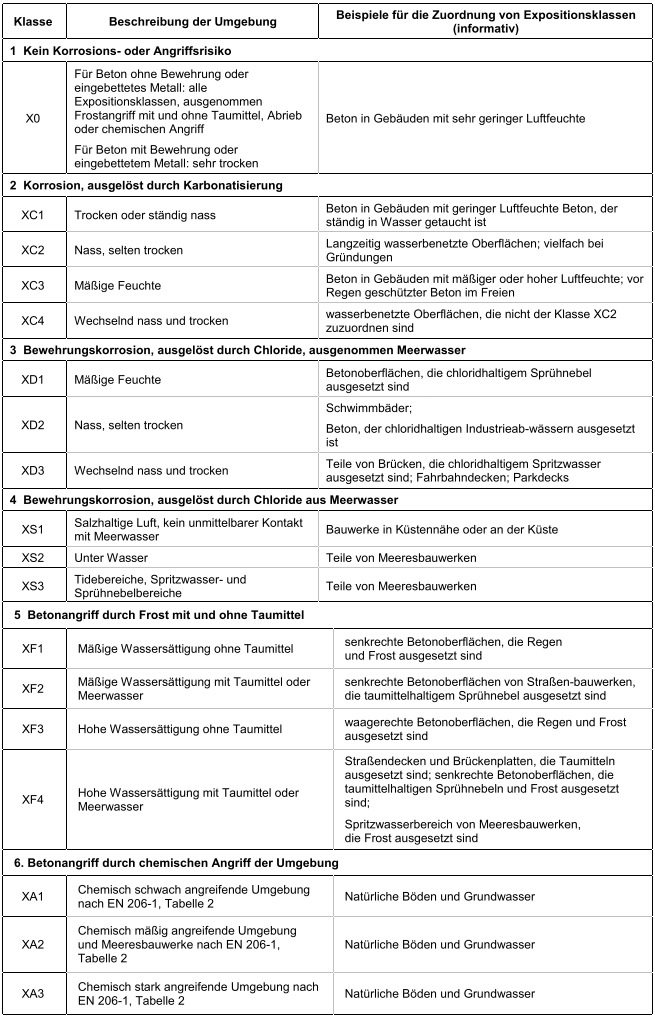
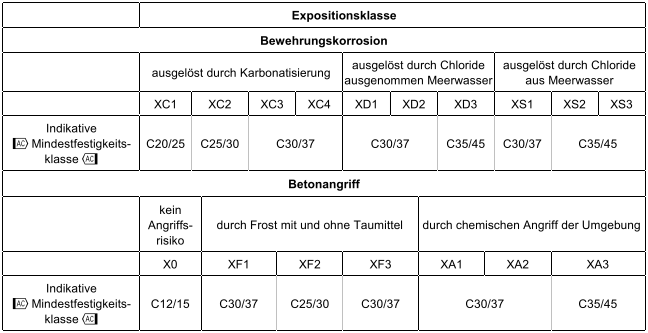
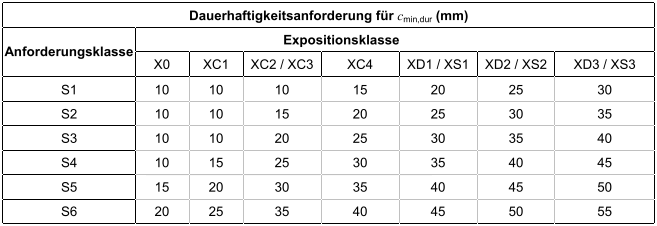
Nach den DAfStb-Richtlinien Wasserundurchlässige
Bauwerke und Betonbau beim Umgang mit
wassergefährdenden Stoffen ist die Wasserundurchlässigkeit
des Betons im Grenzzustand der
Gebrauchstauglichkeit (GZG) nachzuweisen. |
| Die Wasserundurchlässigkeit wird nachgewiesen
über |
|
 |
| Nachweis der Dichtigkeit in ungerissenen Bereichen |
|
 |
| ... Mindestdruckzonendicke |
|
 |
| Rissbreitennachweis als Dichtigkeitsnachweis |
|
|
|
 |
|
| DAfStb-Richtlinien Wasserundurchlässige Bauwerke |
|
|
| Der Nachweis der Dichtigkeit des Betons ist mit
den Bemessungsgrößen aus der "häufigen"
Einwirkungskombination nach DIN 1055-100 zu führen ist.
Der Nachweis der Dichtigkeit in ungerissenen Bereichen entfällt. |
|
| Nachweis der Mindestdruckzonendicke |
|
| Die Druckzonendicke im Zustand 2 wird für
den schlussendlich erforderlichen Bewehrungsquerschnitt
aus dem Dehnungszustand ermittelt. |
| Für den Dichtigkeitsnachweis ist zu belegen |
|
|
|
|
|
| Rissbreitennachweis als Dichtigkeitsnachweis |
|
Alternativ kann ein Rissbreitennachweis
zur Begrenzung der Biegerisse mit der zulässigen
Rissbreite nach
Tab. 2, DAfStb-Richtlinie durchgeführt
werden. |
|
| Detaillierte Beschreibung des <#rissnachweis_basics">Nachweises. |
|
|
|
|
|
|
|
| DAfStb-Richtlinien Betonbau beim Umgang mit wassergefährdenden Stoffen |
|
|
| Die Einwirkungskombination vor der Beaufschlagung
entspricht der "seltenen" Kombination nach DIN 1055-100,
während der Beaufschlagung ist die "quasi-ständige"
Kombination anzusetzen. |
|
| Nachweis der Dichtigkeit in ungerissenen Bereichen |
|
| Zur Sicherstellung der Dichtigkeit muss gelten |
|
| Der Nachweis darf nur in Bereichen angewandt werden, in denen gilt |
|
|
|
|
|
| Nachweis der Mindestdruckzonendicke |
|
| Die Druckzonendicke im Zustand 2 wird für
den schlussendlich erforderlichen Bewehrungsquerschnitt
aus dem Dehnungszustand ermittelt. |
| Für den Dichtigkeitsnachweis ist zu belegen |
|
|
|
|
|
| Rissbreitennachweis als Dichtigkeitsnachweis |
|
| Die Rissbreite ist unter Berücksichtigung
der im Fall der Medienbeaufschlagung wirksamen Beanspruchungen
unter Gebrauchslasten zu begrenzen auf |
|
| Detaillierte Beschreibung des Nachweises. |
|
|
|
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
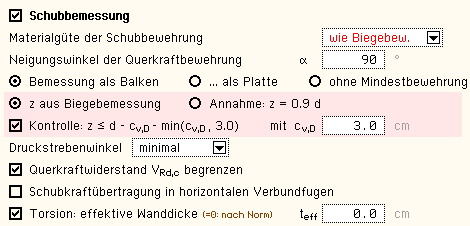
| Schubbemessung bezeichnet die Bemessung
für Querkraft und/oder Torsion. |
| Zunächst wird separat für jede Schnittgröße die
erforderliche Bügel- (Querkraft as,bü) bzw. Bügel-
und Längsbewehrung (Torsion as,büT und As,T)
ermittelt. Anschließend werden die Bewehrungsquerschnitte anteilig
ausgewertet. |
|
| Die Materialgüte der Schubbewehrung kann unabhängig
von der Biegebemessung gewählt werden. |
|
Analog der Biegebemessungsmaterialien steht für senkrecht belastete Flächenträger
(Platte, Faltwerk, Rechteckquerschnitt mit Kennung Platte),
die nach DIN 1045-1, DIN-Fb 102 und EC 2 bemessen werden,
die Bewehrungsausführung mit Gitterträgern zur Verfügung. |
| Gitterträger dienen in erster Linie
dazu, nachträglich mit Ortbeton ergänzte Deckenplatten
(Elementdecken, s.a. Verbundbauteile)
wirtschaftlich und komfortabel herzustellen. |
| G. sind nicht genormt, daher wird in den pcae-Programmen
nicht auf zulassungsspezifische Details eingegangen. |
|
|
| DIN 1045-1, 10.3 und 10.4 / DIN-Fb 102, 4.3.2 und 4.3.3 / EC 2, 6.2 und 6.3 |
|
 |
|
|
Die in die Bemessung
eingehen-
den Schnittgrößen sind Bemessungsgrößen. |
|
| Eigenschaftsblatt aus 4H-EC2QB |
|
 |
|
|
| Querkraftbemessung |
|
Gegenüber den nach DIN 1045 zu führenden Schubspannungsnachweisen sind die Bemessungsmodelle nach
DIN 1045-1 bzw. EC 2 für Bauteile mit und ohne rechnerisch erforderliche Querkraftbewehrung
mechanisch besser nachvollziehbar und damit verständlicher. |
| Die Schubbemessung gliedert sich in die Bemessung für die Querkraft, Torsion und Querkraft mit Torsion. |
| Die Bügelbewehrung kann um den Winkel α gegen die Systemachse
geneigt sein (z.B. Gitterträger). |
|
Zunächst wird der Bemessungswert für den Querkraftwiderstand ohne Querkraftbewehrung
VRd,c
n. EC 2, 6.2.2(1) berechnet. |
| Wenn der Bemessungswert der Querkraft
VEd ≤ VRd,c ist, ist rechnerisch keine Querkraftbewehrung erforderlich. |
| Bei überwiegend auf Biegung beanspruchten stabförmigen Bauteilen
(Balken) ist jedoch grundsätzlich eine Mindestbügelbewehrung für die Querkraft n. EC 2, 9.2.2(5) anzuordnen. |
|
|
| Bemessungswert der ohne
Querkraftbewehrung aufnehmbaren Querkraft |
|
| DIN 1045-1: Der Bemessungswert des Querkraftwiderstands
ergibt sich nach 10.3.3(1) zu |
|
Als wirksame Breite bw wird die minimale Querschnittsbreite in Höhe der
resultierenden inneren Schnittgrößen
(entweder res. Betondruckkraft oder res. Stahlzugkraft) betrachtet. |
| Der VRd,ct -Wert darf auf einen Mindestwert (nicht DIN 1045-1 (7.01)) von |
|
begrenzt werden. Bei einer Bemessung nach DIN 1045-1 (7.01) kann der Mindestwert nach
DIN-Fb 102
berücksichtigt werden. |
|
| EC 2:
Der Bemessungswert des Querkraftwiderstands ergibt sich nach 6.2.2(1) zu |
|
| Dabei können die Faktoren CRd,c, νmin und k1 einem nationalen Anhang entnommen werden. Empfohlen sind |
|
| Bei der Plattenbemessung als rein
biegebeanspruchtes Bauteil, das bei VEd ≤ VRd,c ohne Mindestbewehrung
auskommt, spielt der Zug-Längsbewehrungsgrad ρl eine entscheidende Rolle. |
Das Programm bietet mehrere Möglichkeiten,
die in die Bemessung eingehende Längsbewehrung zu berücksich-
tigen. Sie kann entweder vom Anwender
direkt vorgegeben (nur in 4H-EC2QB als Asl im Eigenschaftsblatt) oder
aus der Biegebemessung
unter Berücksichtigung der Grundbewehrung (Asl = max (As, As0)) übernommen werden. |
|
|
| Besonderheiten bei der
Schubbemessung unbewehrter Betonquerschnitte. |
|
| Bemessungswert der durch
die Tragfähigkeit der Querkraftbew. begrenzten aufnehmbaren Querkraft |
|
| Wenn dagegen gilt VEd > VRd,c ist eine Querkraftbewehrung
derart vorzusehen, dass VEd < VRd,s (6.2.3) ist. |
|
Der innere Hebelarm z ist eine entscheidende
Größe bei der Querkraftbemessung und kann auf drei
verschiedene
Arten angenommen werden |
 |
| z aus der Biegebemessung des zugehörigen N,M-Lastfalls |
|
 |
| n. 6.2.3(1) (nur bei geringer Normalkraftbeanspruchung sinnvoll) mit |
|
|
 |
| z aus der Biegebemessung (wie 1.) mit der Einschränkung aus 6.2.3(1) |
|
|
|
|
| Besonderheiten |
 |
| ist der zugehörige N,M-Lastfall Null, wird angenommen |
|
| bei Kreisquerschnitten |
|
|
 |
| ist der Querschnitt
überdrückt, wird der innere Hebelarm
berechnet zu |
|
|
 |
| ist der Querschnitt überzogen, ergibt sich z zum Abstand der Bewehrungslagen |
|
 |
| ist cv,D = 0, wird vereinfachend angenommen |
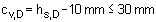 |
| (Annahme einer einlagigen Druckbewehrung mit dem
Längsstabdurchmesser ds = 20 mm) |
|
|
 |
| bei Kreisquerschnitten ist bei überzogenem Querschnitt |
|
|
 |
bei Kreisquerschnitten wird die wirksame Querschnittsbreite
bw auf die Breite in Höhe
der äußersten
Bewehrungslage begrenzt |
|
|
|
| Der Bemessungswert der aufnehmbaren
Querkraft VRd,sy (as,bü)
ist dabei abhängig von der Neigung der Querkraftbewehrung
α und der Neigung der Druckstreben cot θ. |
α und θ sind im Eigenschaftsblatt
vorzugeben, werden aber programmintern auf ihre
Grenzwerte hin überprüft
und bei Bedarf angepasst
(s. Ausgabeprotokoll). |
|
| Grenzwerte der Neigung der Querkraftbewehrung 45° ≤ α ≤135°. |
|
|
| Grenzwerte der Neigung der Druckstreben |
|
| DIN 1045-1 und EC 2, NA-DE |
|
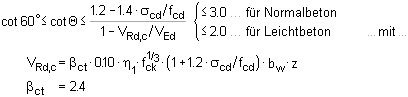 |
|
| Ein Druckstrebenwinkel größer als
45° sollte nur in Ausnahmefällen, z.B. bei geneigter
Querkraftbewehrung verwendet werden. |
| Bei Zuglängsbelastung darf der Druckstrebenwinkel
jedoch nicht größer als 45° angenommen werden. |
|
|
 |
Je kleiner θ gewählt wird, desto weniger Bewehrung ergibt sich. Allerdings
wirkt sich θ umgekehrt propor-
tional bei der Berechnung der
Verankerungslängen der Längsbewehrung (Versatzmaß, 9.2.1.3(2)) aus! |
|
|
|
|
| Vereinfachend darf nach EC 2, NA-DE, NDP zu 6.2.3(2) angenommen werden für |
 |
| reine Biegung oder
Biegung und Längsdruckkraft |
|
|
 |
| Biegung und Längszugkraft |
|
|
|
|
| EC 2 |
| Der landesspezifische Wert für
cot θ darf einem nationalen Anhang entnommen werden (6.2.3(2)). |
| Empfohlen ist |
|
|
| Bemessungswert der durch
die Druckstrebenfestigkeit begrenzten aufnehmbaren Querkraft |
Allerdings darf der Bemessungswert der einwirkenden Querkraft in keinem Querschnitt
des Bauteils den
Wert VRd,max überschreiten. |
|
| DIN 1045-1: Nach 10.3.4(6) gilt |
|
| EC 2: Nach 6.2.3(3) und (4) gilt |
|
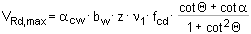 |
|
| Die landesspezifischen
Werte ν1 und αcw dürfen einem nationalen Anhang entnommen werden. |
| Empfohlen sind |
|
| NA-DE |
|
|
| Wird jedoch eine Grundbewehrung asb0 vorgegeben, die größer als die erforderliche
Querkraftbewehrung ist, darf die Druckstrebenneigung
cot Θ zur Ermittlung von VRd,max um den Anteil erf asb/asb0 reduziert werden. |
|
|
| Ausnutzungsgrad des Querschnitts infolge Querkraftbeanspruchung |
| Die Querkraftbewehrung kann aus Bügeln oder - bei geringerer Ausnutzung
VEd/VRd,max - aus aufgebogenen Stäben der Längsbewehrung
bestehen. Außerdem sind der maximale Längs- und Querabstand der Querkraftbewehrung zu beachten!
In Analogie zum Schubbereich der DIN 1045 ('88) werden daher Ausnutzungsbereiche
definiert, die die Beanspruchung des Querschnitts kennzeichnen. |
|
| DIN 1045-1 - Tab. 31 |
|
|
|
| EC 2 - n. 9.3.2(3) |
|
|
| EC 2, NA-DE - Tabelle NA.9.1+2, NDP zu 9.2.2(6)+(8) |
|
|
|
|
|
|
|
| Mindestquerkraftbewehrung |
|
| DIN 1045-1 - Nach 13.2.3(5), Tab. 29 ist bei überwiegend
auf Biegung beanspruchten Bauteilen ist eine Mindestquerkraftbewehrung vorzusehen in Höhe von |
|
|
| EC 2 - Nach 9.2.2(5) darf die Mindestquerkraftbewehrung
für Balken einem nationalen Anhang entnommen werden. Empfohlen ist |
|
Platten und Faltwerke bilden als Flächenträger
mit b/h > 5 ebenso wie Stützen und Wände als Druckglieder
mit ed/h < 3.5 eine Ausnahme. |
|
|
|
|
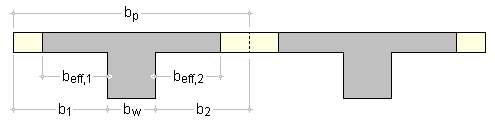
| Anschluss der Gurte an den Balkensteg |
|
| Bei Plattenbalken und Doppel-T-Querschnitten
ist der Anschluss der abstehenden Querschnittsteile
(Gurte) an den Balkensteg zu bemessen (nur 4H-EC2QB, 4H-EC2QB). |
| Nähere Informationen finden Sie hier. |
|
|
|
|
| Schubkraftübertragung in Fugen |
|
Für einige Querschnittstypen ist es
möglich, die zumeist erhöhte Querkraftbewehrung
im Fugenbereich
zu berücksichtigen. |
| Nähere Informationen finden Sie hier. |
|
|
|
|
| Besonderheiten bei zweiachsiger Querkraftbeanspruchung (genigter Querkraft) |
|
| Die Bemessung kann auf zwei Arten erfolgen |
|
| Bemessung der Querkraftkomponenten |
| Die Querkraft wird in ihre Komponenten
zerlegt und in den entsprechenden Richtungen (ggf.
einschließlich des Torsionsmoments) einachsig bemessen. |
| Die Vorstellung beruht dabei darauf,
dass jede Querkraftkomponente unabhängig von
der anderen jeweils eine Bügelschenkelrichtung abdeckt. |
| Das Bemessungsergebnis ist demnach
das Maximum aus den Einzelbemessungen. |
|
| Bemessungsansatz von Peter Mark |
| Unter den Bedingungen |
 |
|
 |
|
 |
| innerer Hebelarm aus Biegebemessung |
|
|
| kann der Ansatz von P. Mark durchgeführt werden. |
|
| Vergrößerung der Bügelkräfte um den Faktor |
|
| Verringerung der maximalen Druckstrebentragfähigkeit um den Faktor |
|
| mit der dimensionslosen Querkraftneigung |
|
| Aus Kompatibilitätsgründen
(zur einachsigen Querkraftbemessung) ergibt sich
die wirksame Querschnittsbreite zu |
|
 |
Je schiefwinkliger die Querkraft
wirkt, um so mehr Bewehrung ergibt sich gegenüber
der "Komponenten"-
methode. Untersuchungen haben gezeigt, dass
die nach der "Komponenten"methode
ermittelte Bewehrung ggf. zu gering ist, da
das zweiachsige Tragverhalten des Querschnitts nicht erfasst wird. |
|
|
|
|
|
|
| Torsionsbemessung |
|
| Bei der Bemessung für Torsion ist
bei Vollquerschnitten i.d.R. nur die St. Venant'sche Torsion zu betrachten. |
| Die Torsionstragfähigkeit kann unter
Annahme eines dünnwandigen, geschlossenen Querschnitts mit der Ersatzwanddicke teff = 2 · d1 nachgewiesen werden. |
| Bei Hohlquerschnitten darf teff nicht größer sein als die vorhandene Wanddicke. |
| Bei schmalen Querschnitten mit teff > bw / 2 wird gesetzt teff = 2 · (bw / 2 - d1). |
| EC 2 |
|
|
| Zunächst ist zu überprüfen,
ob Torsionsbewehrung erforderlich ist (nicht DIN-Fb 102). |
|
| DIN 1045-1 - Dies geschieht nach Abschnitt
10.4.1(6) für einen näherungsweisen rechteckigen Vollquerschnitt mit |
|
| EC 2 - Bei näherungsweise
rechteckigen Vollquerschnitten ist nur die Mindestbewehrung erforderlich, wenn gilt |
|
|
| Bemessungswert des durch
die Tragfähigkeit der Bew. begrenzten aufnehmbaren Torsionsmoments |
|
| Kann der Nachweis nicht erbracht werden, ist mit 6.3.2(3)
die Bewehrung so zu ermitteln, dass gilt TEd = TRd,sy. |
Der Bemessungswert des aufnehmbaren Torsionsmoments TRd,sy (asbü,T und As,T ist dabei abhängig von der
Neigung der Druckstreben cot θ. |
|
DIN 1045-1 und EC 2, NA-DE -
Die Neigung der Druckstreben ist für die Schubkraft in der Wand infolge
Querkraft und Torsion |
|
| zu ermitteln. Sie ist für den
Querkraftnachweis gleichermaßen anzuwenden. |
| Berechnung des Bemessungswerts des aufnehmbaren Torsionsmoments |
|
|
| Bemessungswert des durch
die Druckstrebenfestigkeit begrenzten aufnehmbaren Torsionsmoments |
|
| Allerdings darf der Bemessungswert
des einwirkenden Torsionsmoments in keinem Querschnitt
des Bauteils den Wert TRd,max überschreiten. |
|
| DIN 1045-1 |
|
|
| EC 2 |
|
|
| Bemessung für Querkraft und Torsion |
|
| Die maximale Tragfähigkeit bei kombinierter Beanspruchung aus Querkraft und
Torsion wird durch die Druckstrebentragfähigkeit begrenzt mit |
|
| DIN 1045-1 und EC 2, NA-DE |
|
| EC 2 |
|
|
| Hauptdruckspannungsnachweis |
|
Wände oder ähnliche, hauptsächlich
über Normalkraft abtragende Bauteile sind bezüglich
ihrer
Hauptdruckspannung zu überprüfen. |
| Nach 6.5.2 ist der Bemessungswert der Druckstrebenfestigkeit begrenzt durch |
|
|
|
|
|
|
|
|
|
 |
|
| Die Bügelbewehrung steht senkrecht auf der Längsbewehrung. |
Der Sicherheitsbeiwert für Schub beträgt
γSchub = 1.75. |
|
| Abb. Eigenschaftsblatt aus 4H-EC2QB |
|
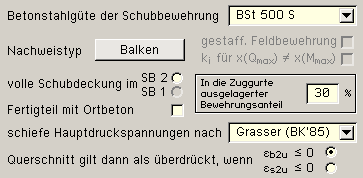 |
|
|
| Querkraftbemessung |
|
Die Querkraftbemessung hängt entscheidend
vom Querschnittszustand (Zustand 1 – ungerissen, voll überdrückt
oder Zustand 2 – gerissen) ab. |
| Bei einem gerissenen Querschnitt wird
nach Mörsch zunächst der Grundwert der Schubspannung
τ0 = Q/(b0·z) ermittelt, der von der Lage der Dehnungsnulllinie
(kx und kz entweder ermittelt aus der Biegebemessung oder unter Annahme eines
reinen Biegezustands) abhängig ist. |
| Als wirksame Breite b0 wird die Querschnittsbreite in Höhe der Dehnungsnulllinie betrachtet. |
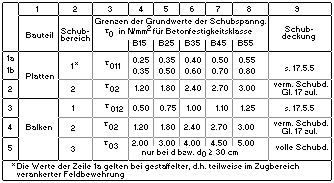
Die einzuhaltenden Grenzen der Grundwerte
der Schubspannung (Tab. 13) richten sich danach,
ob das Bauteil
als Platte (keine Querkraftbewehrung
im Schubbereich 1) oder als Balken (Mindestquerkraftbewehrung im
Schubbereich 1) betrachtet wird. |
| Tab. 13: Grenzen der Grundwerte der
Schubspannung τ0 in N/mm2 unter Gebrauchslast |
|
| Bei Platten geht zusätzlich ein, ob
die Feldbewehrung gestaffelt eingelegt wird, und
ob max lQl und max lMl an der gleichen Stelle auftreten
(Faktor ki). |
| Reduzierte Grenzschubspannungen ergeben
sich bei einer Ergänzung von Fertigteilen mit Ortbeton. |
Die Größe von τ0 ist
ausschlaggebend für den Schubbereich und damit für den Bemessungswert τ,
für den die Bügelbewehrung as,bü bestimmt wird. |
Für spezielle Anwendungen kann die
Schubspannung auch voll abgedeckt werden. Unabhängig
von den Schubbereichen wird bei Platten und Balken
ohne Abminderung bemessen. Es besteht die Möglichkeit,
entweder nur die Schubbereiche 2+3 oder alle Schubbereiche
voll abzudecken. |
Bei Plattenbalken und Doppel-T-Querschnitten
werden die abstehenden Querschnittsteile (Gurte)
nach 18.8.5
(nur 4H-EC2QB und 4H-DULAB)
zusätzlich bemessen. Dazu ist für die Bemessung
des Zugflansches der in
die Gurte ausgelagerte Bewehrungsanteil anzugeben. |
| Bei Flächentragwerken (Platte oder
Faltwerk) sollte möglichst auf eine Schubbewehrung
verzichtet werden. |
| Da die Querkraftverteilung i. A. nicht
mit der Bewehrungsanordnung übereinstimmt, wird
die Hauptquerkraft nachgewiesen und nach Bedarf
bemessen. |
Dazu werden die benötigten Parameter
näherungsweise ermittelt entweder als Minimalwerte
sämtlicher
zu einem Lastfall gehörender Transformationskombinationen
(Standardfall) oder unter Annahme eines reinen Biegezustands (s.o.). |
|
Ist der Querschnitt überdrückt
(d.h. die maximale Dehnung ist entweder εb2 ≤ 0 oder εs2 ≤ 0, frei
eingebbar),
wird für die Hauptzugspannung nach Mohr τ = σ1I bemessen. |
| Diese ergibt sich für baupraktische Zwecke ausreichend genau zu |
|
| Für eine genauere Berechnung s. Friemann. |
|
|
|
|
| Nachweis der schiefen Hauptdruckspannungen |
|
Außerdem ist bei erfolgreicher Querkraftbemessung
der Nachweis der schiefen Hauptdruckspannung (wahlweise
nach Heft 400, DAfStb oder nach Grasser (BK'85)
unter Berücksichtigung des Heftes 320, DAfStb) zu führen. |
| Literaturangaben s. unten. |
|
| Verfahren nach Heft 400, DAfStb |
|
| Bei der Berechnung der schiefen Hauptdruckspannungen wird eine Neigung
der Druckstrebe von 45° im Zustand 1 zugrunde gelegt,
so dass sich σ1I folgendermaßen berechnet |
|
Bei der Annahme lotrechter Bügel und bei einer empfohlenen Druckfeldneigung
von tan ϑ = 0.4 berechnet sich
aus τ0 die schiefe Hauptdruckspannung σ2II zu |
|
| Die Begrenzung der Hauptdruckspannung
wird n. DIN 1045 angegeben mit σ2II ≤ 2 · τ03. |
|
| Verfahren nach Grasser & Heft 320, DAfStb |
|
| Die Ermittlung der Neigung des Druckfelds im Zustand 2 erfolgt zu |
|
| Die Berechnung von σ2II erfolgt bei Annahme lotrechter Bügel wie im Heft
400 mit dem neu berechneten Neigungswinkel θ |
|
| Nach Heft 320 sind auch Neigungswinkel von tan ϑ < 0.4 zugelassen. |
|
|
|
|
| Torsionsbemessung |
|
| Die Torsionsbemessung ist nur dann
durchzuführen, wenn der Grundwert τT die Werte 0.25 τ02 (s. Tab.
13) überschreitet. |
| Der Grundwert ist mit den Querschnittswerten
nach Zustand 1 zu ermitteln und darf die Werte τ02 nicht überschreiten. |
Aufgrund des gedachten räumlichen
Fachwerks mit unter 45° geneigten Druckstreben ergeben sich eine
Bügelbewehrung as,büT und eine Längsbewehrung As,T. |
|
|
|
|
| Bemessung für Querkraft und Torsion |
|
| Der Nachweis von Querkraft und Torsion ist erfüllt, wenn gilt |
|
| Die Bewehrungsanteile aus den Einzelnachweisen werden folgendermaßen addiert |
|
|
|
|
|
| ComBAR GFK |
|
| Besteht die Längsbewehrung
aus glasfaserverstärktem Kunststoff, darf Schubbewehrung
rechnerisch nicht erforderlich sein. Daraus folgt,
dass die Querkraft den Bemessungswert
der ohne Querkraftbewehrung aufnehmbaren Querkraft
n. EC 2, 6.2.2 nicht überschreiten darf. |
| Es gelten für Gl. 6.2a die Parameter
CRd,c = 0.138/γc und σcp = 0. |
|
|
|
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| DIN 1045-1, 10.3.5 / EC 2, 6.2.4 |
|
| Bei Plattenbalken und Doppel-T-Querschnitten
ist bei ausgeprägten Gurtplatten der Anschluss der
abstehenden Querschnittsteile an den Balkensteg nachzuweisen. |
| Dazu ist der Bemessungswert der einwirkenden Längsschubkraft zu ermitteln aus |
|
| bei Anschluss eines Druckgurts |
|
| bei Anschluss eines Zuggurts |
|
Die Wahl der maßgebenden Länge av,
innerhalb der die Längsschubkraft als konstant angenommen werden
darf,
sollte nicht größer sein als der halbe Abstand zwischen
Momentennullpunkt und Momentenhöchstwert bzw. nennenswertem
Querkraftsprung. |
|
| Abb.: Eigenschaftsblatt aus 4H-EC2QB |
 |
|
|
| Für diese Bemessungsquerkraft erfolgt
der Nachweis der Druckstrebenfestigkeit (s. auch Querkraftbemessung) mit |
|
| Die Anschlussbewehrung (Querbewehrung in der Gurtplatte) ergibt sich zu |
|
| Vereinfachend wird für die Neigung der Druckstreben beim Anschluss eines Druckgurts |
|
| und beim Anschluss eines Zuggurts angesetzt |
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
Einachsig gespannte Bauteile (Querschnitte unter
einachsiger Biegung und Querkraft, nicht Kreis(ring)) und
Platten (Elementdecken) können als Verbundbauteile von Fertigteil
mit Ortbetonergänzung oder als zwei
nacheinander betonierte Ortbetonabschnitte ausgeführt werden. |
|
|
|
| Abb. Eigenschaftsblatt aus 4H-EC2QB |
|
|
| DIN 1045-1 (7.01), 10.3.6 |
|
 |
|
| Der Bemessungswert der in der Kontaktfläche
zwischen Ortbeton und Fertigteil oder in nachträglich ergänzten
Querschnitten zu übertragenden Schubkraft je Längeneinheit wird ermittelt zu |
|
| Ohne Anordnung einer Verbundbewehrung
darf vEdj den folgenden Bemessungswert der aufnehmbaren
Schubkraft in Fugen von Verbundbauteilen nicht überschreiten |
|
| In bewehrten Fugen von Verbundbauteilen
beträgt der Bemessungswert der aufnehmbaren Schubkraft |
|
 |
| Wenn max cot θj,zul <
min cot θj,zul (d.h. der Bruch < 1.0)
ist, wird ein Fehler ausgewiesen, da der Nachweis der
Verbundfuge nicht zulässig ist. |
| Bei Zugfugen (z.B. in Überzügen)
gilt i.A. σNd = σcd = 0 und β1 = 1, so dass der Bruch nur
bei verzahnt ausgebildeten Fugen größer als
der Grenzwert 1.0 wird! |
|
|
|
|
|
|
| DIN 1045-1 (8.08), 10.3.6 |
|
 |
|
| Der Bemessungswert der in der Kontaktfläche
zwischen Ortbeton und Fertigteil oder in nachträglich ergänzten
Querschnitten zu übertragenden Schubkraft je Längeneinheit wird ermittelt zu |
|
| Der Bemessungswert der aufnehmbaren Schubkraft in Fugen wird ermittelt zu |
|
| Wenn σNd eine Zugspannung ist,
ist bei glatten und rauen Fugen cj = 0 zu setzen. |
| Wenn die Fuge unter dynamischer Belastung steht, ist cj = 0 zu setzen. |
|
| Die maximal aufnehmbare Schubkraft beträgt |
|
|
|
|
|
|
 |
|
| Der Bemessungswert der in der Kontaktfläche
zwischen Ortbeton und Fertigteil oder in nachträglich ergänzten
Querschnitten zu übertragenden Schubkraft je Längeneinheit wird ermittelt zu |
|
| Der Bemessungswert des Schubkraftwiderstands
in der Fuge ist gegeben durch (Druckstrebenwinkel θ = 45°) |
|
| Wenn σNd eine Zugspannung ist, ist c = 0 zu setzen. |
| Wenn die Fuge unter dynamischer Belastung steht, ist c zu halbieren. |
| Nach NA-DE, Kap. 6.2.5(1), Gl. (2.25) darf der Bewehrungsanteil erhöht
werden auf ρ · fyd · (1.2 · μ · sin α + cos α). |
|
|
|
|
|
 |
|
Soll die Schub- und Verbundbewehrung
mit Gitterträgern (einzugeben als Materialgüte
der Schubbewehrung,
nur plattenartige Querschnitte) ausgeführt werden, wird programmintern
eine Zugfestigkeit der Bewehrung von
fyk = 420 N/mm2 (glatte Gitterträgerdiagonalen
werden bemessen wie eine aufgebogene Längsbewehrung) angesetzt. |
| Weitere Einschränkungen sind gegeben mit |
|
Die zulässige Größe des Druckstrebenwinkels
ist in den jeweiligen Zulassungen geregelt; daher wird bei
Gitterträgern max cot θj,zul nicht überprüft. |
|
| Weiterhin ergibt sich die Grenze
des Ausnutzungsbereichs 1 (d.h. bis zu welcher Belastung
die Querkraftbewehrung als reine Gitterträgerkonstruktion
ohne Bügel ausgeführt werden darf) zu |
|
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
| Das Ziel beim Entwurf von Stahlbetonbauteilen
ist die Begrenzung der entstehenden Rissbreiten auf ein Maß,
das die ordnungsgemäße Funktion und Dauerhaftigkeit eines Bauwerks
gewährleistet. |
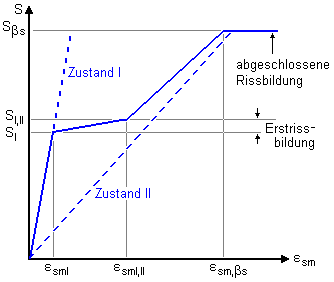
Wird ein Stahlbetonstab einer Zugbelastung ausgesetzt,
so ergibt sich (idealisiert) folgendes
Last-Verformungs-Diagramm |
|
|
Zunächst ist der Querschnitt ungerissen
(Zustand 1)
bis es bei εsmI unter SI zum ersten Riss kommt. |
| I.d.R. hat der Bewehrungsgrad hier keinen
nennenswerten Einfluss auf die Steifigkeit des Trägers. |
| Danach nimmt die Rissanzahl bei weiterer
Lastzunahme stark zu, bis bei εsmI,II unter SI,II die Erstrissbildung abgeschlossen
ist. |
| Die Steifigkeit des Bauteils nimmt mit zunehmender
Belastung ständig ab und nähert sich der Steifigkeit des
reinen Zustands 2 an. |
| Ab jetzt ändert sich die Rissanzahl wenig,
bis bei εsm,βs unter Sβs entweder die Rissbildung abgeschlossen ist oder der Träger
versagt. |
| Die Abnahme der Steifigkeit resultiert vor
allem aus der lokalen Schädigung des Verbunds. |
|
 |
|
|
| In pcae-Programmen werden - je nach Ausbaustufe
- folgende Nachweisverfahren angeboten: |
|
|
 |
| Norm (ohne direkte Berechnung der Rissbreite) |
|
 |
| Norm (Berechnung der Rissbreite,
nicht DIN 1045) |
|
 |
|
 |
|
|
|
|
In Abhängigkeit der nachfolgend beschriebenen
Parameter wird zunächst der minimale Bewehrungsgrad in der
Zugzone bestimmt. |
| Anschließend wird überprüft, ob die erforderlichen
Grenzdurchmesser oben und unten für die maßgebende Risslast
eingehalten werden. Ist der Nachweis nicht erfüllt, werden die
Bewehrungsquerschnitte entsprechend erhöht. |
|
 |
| Beim Nachweis der zulässigen
Rissbreite für Plattenbalken- und Doppel-T-Querschnitte
wird die Einflussbreite der Bewehrung auf Stegbreite
zzgl. 3-fachem Stahlrandabstand begrenzt. |
|
|
|
| Folgende Parameter sind festzulegen |
|
|
 |
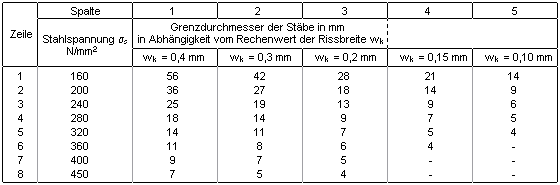
| der maximale Stabdurchmesser der Bewehrung ds,gr |
|
 |
| die rechnerische Rissbreite wcal (DIN 1045:
über die Umweltbedingung nach Tab. 10) |
|
 |
| das Verbundverhalten zwischen Bewehrung und Beton (nur Schießl
und Noakowski) |
|
 |
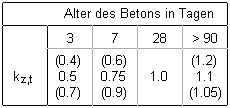
| das maßgebende Betonalter durch den Faktor kz,t |
| Faktor kz,t für normal erhärtende
Zemente, übliche Bauteilabmessungen und unter Normaltemperatur
der Luft. |
Die unteren Klammerausdrücke gelten
für schnell erhärtende Zemente, sehr hohe Umgebungstemperaturen
und/oder massige Bauteile;
die oberen für langsam erhärtende Zemente und/oder
niedrige Umgebungstemperaturen während des Erhärtens. |
|
 |
|
|
|
 |
| die Art der Zwangsbeanspruchung, die den Beiwert für
nichtlineare Eigenspannungen beeinflusst. Der Zwang kann selbst- oder außerhalb induziert
sein (nur bei ,Mindestbewehrung', nicht DIN 1045). |
|
 |
| die Form der Spannungsverteilung durch den Zwang, die unterschiedlich
ist bei zentrischem oder Biegezwang (nur bei ,Mindestbewehrung', nicht DIN 1045) |
|
 |
| die Zwangsschnittgröße
Nc im Schwerpunkt des Betonquerschnitts. (nur
bei ,Mindestbewehrung', nicht DIN 1045) |
|
 |
| eine Kennung für langsam erhärtenden Beton (nur bei ,Mindestbewehrung',
nicht DIN 1045) |
|
 |
| den Beiwert für den Dauerstandseffekt für langfristige oder kurzzeitige Lasteinwirkung (nur bei ,Begrenzung
der Rissbreite', nicht DIN 1045) |
|
|
|
 |
| Der kzt-Wert bezieht sich
auf den Betrachtungszeitpunkt der Nachweisführung.
Die Berechnung der Mindestbewehrung wird zum Zeitpunkt
der Erstrissbildung mit kzt, der Nachweis
zur Begrenzung der Rissbreite wird nach abgeschlossener
Rissbildung mit kzt0 geführt. |
|
|
|
|
 |
|
| Beim Rissbreitennachweis ist zwischen dem
Zustand der Bildung von Einzelrissen und dem Zustand mit
abgeschlossenem Rissbild zu unterscheiden. |
|
| Zur Aufnahme von Zwangseinwirkungen
und Eigenspannungen ist eine Mindestbewehrung anzuordnen, die unter Berücksichtigung der
Anforderungen an die Rissbreitenbegrenzung für
die Schnittgrößenkombination zu bemessen
ist, die im Bauteil zur Erstrissbildung führt. |
| Die Rissbreiten infolge einer Lastbeanspruchung
sind vor allem von der vorhandenen Spannung in der Bewehrung
und von deren Anordnung im Querschnitt abhängig. |
| Deshalb sind die Stabdurchmesser oder die
Stababstände der gewählten Bewehrung in Abhängigkeit der
Spannung zu begrenzen. |
| Es erfolgt der Nachweis zur Einhaltung der
Stabdurchmesser (der Nachweis zur Einhaltung der Stababstände
liegt auf der unsicheren Seite, s. Heft 525, DAfStb). |
|
| Abb. Eigenschaftsblatt
aus 4H-EC2QB |
|
 |
|
|
|
| Mindestbewehrung für die Begrenzung der Rissbreite (EC 2, 7.3.2) |
 |
 |
Berechnung der auf die Zugzone
nach Zustand 1 bezogenen Bewehrung in cm2 |
|
|
| |
 |
|
|
 |
Berechnung des Grenzdurchmessers
der Bewehrung |
|
|
|
|
|
|
| Mindestbewehrung bei dicken Bauteilen (EC 2, NA-DE, NCI zu 7.3.2 (3)) |
 |
| Es kann günstiger sein bei zentrischem
Zwang stattdessen folgende Bewehrung einzulegen |
|
|
|
|
|
| Begrenzung der Rissbreite ohne direkte Berechnung (EC 2, 7.3.3) |
 |
|
| Die Spannungen werden auf Gebrauchslastniveau mit den gewählten
Spannungsdehnungslinien (s. Materialeigenschaften) ermittelt. |
|
|
|
|
|
| Berechnung der Rissbreite (EC 2, 7.3.4) |
 |
|
|
| Zur Ermittlung der Mindestbewehrung
kann die Formel umgestellt und nach As aufgelöst werden |
|
|
| Diese Variante zur Ermittlung der
Mindestbewehrung wird in den pcae-Programmen nicht angeboten. |
|
|
| Die Spannungen werden auf Gebrauchslastniveau mit den gewählten
Spannungsdehnungslinien (s. Materialeigenschaften) ermittelt. |
|
| DIN 1045-1 / DIN-Fb 102 |
 |
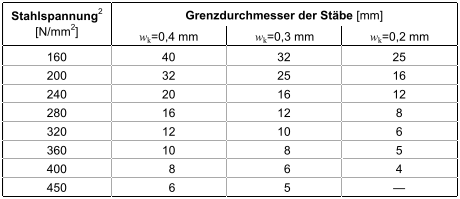
| Tab. 20: Grenzdurchmesser ds* bei Betonstählen in mm
(die Tab.-Werte sind ermittelt mit |
|
|
Die mindestens einzuhaltende Rissbreite
wk ist abhängig von der Expositionsklasse,
in der sich das Bauteil befindet
(s. Tab. 18 und 19). |
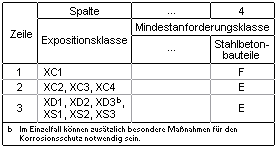
| Tab. 19: Mindestanforderungsklassen in Abhängigkeit von der Expositionsklasse (Auszug) |
|
| Tab. 18: Anforderungen an die Begrenzung der Rissbreite (Auszug) |
|
 |
| Wenn der Zeitpunkt der Erstrissbildung
nicht mit Sicherheit innerhalb der ersten
28 Tage festgelegt werden kann, sollte mindestens
eine effektive Betonzugfestigkeit von 3 N/mm2 für Normalbeton und 2.5 N/mm2 für Leichtbeton angenommen werden. |
| Im Programm kann eingestellt
werden, ob für kzt ≥ 1
min fct,eff eingehalten werden
soll. |
|
|
|
|
| EC 2 |
 |
| Tab. 7.2N: Grenzdurchmesser ds* bei Betonstählen in mm |
|
| Die mindestens einzuhaltende Rissbreite
wk ist abhängig von der Expositionsklasse,
in der sich das Bauteil befindet. |
| Tab. 7.1N (EC 2-1-1): Empfohlene Werte für wmax (Auszug) |
|
| Tab. 7.101N (EC 2-2): Empfohlene Werte für wmax (Auszug) |
|
 |
| Wenn der Zeitpunkt der Erstrissbildung
nicht mit Sicherheit innerhalb der ersten
28 Tage festgelegt werden kann, sollte mindestens
eine effektive Betonzugfestigkeit von 3 N/mm2 für Normalbeton und 2.5 N/mm2 für Leichtbeton angenommen werden. |
| Im Programm kann eingestellt
werden, ob für kzt ≥ 1
min fct,eff eingehalten werden
soll. |
|
|
|
|
|
|
|
 |
|
| Der Rissbreitennachweis
gliedert sich in zwei Teile. |
In oberflächennahen Bereichen von Stahlbetonbauteilen,
in denen Betonzugspannungen aus innerem Zwang entstehen
können, ist
i. A. eine Mindestbewehrung einzulegen. |
| Wird diese nicht durch die Biegebewehrung
abgedeckt, ist der Bewehrungsgrad entsprechend zu erhöhen. |
|
| Die Rissbreiten infolge einer Lastbeanspruchung
richten sich nach Regeln für die statisch erforderliche
Bewehrung und sind vor allem von der vorhandenen Spannung
in der Bewehrung und von deren Anordnung im Querschnitt
abhängig. |
| Deshalb sind die Stababstände bzw. die Stabdurchmesser
der gewählten Bewehrung in Abhängigkeit der Spannung zu
begrenzen. |
| Es erfolgt der Nachweis zur Einhaltung der
Stabdurchmesser. Werden sie durch die Biegebewehrung nicht
eingehalten, ist der Bewehrungsgrad entsprechend zu erhöhen. |
|
| Abb. Eigenschaftsblatt aus 4H-EC2QB |
|
 |
| |
|
|
| Mindestbewehrung (17.6.2) |
 |
 |
|
| Bei Zwang im frühen Betonalter kz,t ≈ 0.5 darf mit der
dann vorhandenen geringeren wirksamen Betonzugfestigkeit gerechnet werden βbZw = kz,t · βbZ. Dann ist jedoch
der Grenzdurchmesser (s.o.) im Verhältnis βbZw / 2.1 zu verringern. |
|
|
|
|
|
|
| Regeln für die statisch erforderliche Bewehrung (17.6.3) |
 |
 |
|
Die Spannungen werden mit dem Parabel-Rechteck-Diagramm
für Beton und der bilinearen Spannungsdehnungslinie
für die Bewehrung ermittelt (s. Materialeigenschaften). |
|
| Tab. 14: Grenzdurch-messer ds,gr in mm |
|
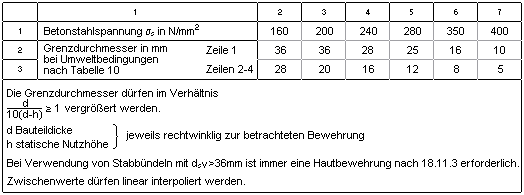 |
|
|
|
|
|
|
|
|
|
|
 |
|
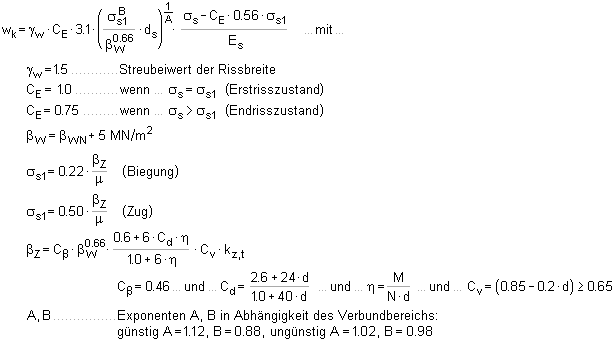 |
|
 |
| Wenn der Zeitpunkt der Erstrissbildung nicht
mit Sicherheit innerhalb der ersten 28 Tage festgelegt
werden kann, sollte mindestens die Festigkeit eines B35
angenommen werden. Im Programm kann eingestellt werden,
ob für kzt ≥ 1 min βbz eingehalten werden soll. |
|
|
|
|
|
|
 |
|
| Der Nachweis bereitet bei Kreisquerschnitten unter
Biegebeanspruchung Schwierigkeiten, da das Verfahren mit Ausnahme
der ÖNorm nur für Rechteckquerschnitte gültig
war, bei denen alle Bewehrungsstäbe der Zugzone die gleiche
Spannung haben. |
| Aus diesem Grund ist auch der auf die Zugzone
bezogene Bewehrungsgehalt nicht eindeutig. |
| Zur realistischen Bemessung sind daher für
die Verfahren zur direkten Berechnung der Rissbreite folgende
Modifikationen implementiert worden (s. hierzu Bergfelder/Dittfach). |
| Die Stahlspannungen werden bei Biegung über
die gemittelten Zug-Stahldehnungen, bei zentrischem Zug über
die maximale Stahldehnung ermittelt. |
|
|
|
| EC 2 / DIN 1045-1 / DIN-Fb 102 / Schießl |
 |
|
|
|
| Schießl, Noakowski |
 |
|
| |
Biegezwang |
σr wird mit 2.2 multipliziert |
| |
Zugzwang |
σr wird mit 2.0 vervielfacht |
 |
| Da diese Anpassungen nur bei
der 'Berechnung der Rissbreiten' wirken, ergibt
sich u.U. bei der tabellenorientierten Nachweisführung
(bezogen auf einen Rechteckquerschnitt) zu
wenig Bewehrung! |
|
|
|
|
|
|
| besondere Hinweise bei Wänden |
 |
| Bei schubfest mit dem Fundament verbundenen Wänden darf die
Mindestbewehrung aus Zwang aufgrund
der
rissverteilenden Wirkung des Fundaments
bis zu einer Wandhöhe von h/4 oberhalb des Fundaments auf
die Hälfte reduziert werden. |
|
|
|
|
| ComBAR GFK |
 |
Besteht die Längsbewehrung
aus glasfaserverstärktem Kunststoff, ist die
Bestimmung der Mindestbewehrung nach
EC 2, 7.3.2
und die Begrenzung der Rissbreite ohne direkte Berechnung
nach 7.3.3 nicht zulässig. |
| ComBAR GFK darf nur für Stabdurchmesser
8 mm bis 32 mm eingesetzt werden. |
| Die Rissbreite wird nach EC 2, 7.3.4
berechnet, wobei für den maximalen Rissabstand sr,max die Beiwerte k1 = k2 = 1, k3 = 0 und k4 = 1 / 2.8 (für Stabdurchmesser
32: k4 = 1 / 2.1) und gesetzt werden. |
|
|
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| Der Nachweis zur Begrenzung der Stahl- und Betondruckspannungen
im Grenzzustand der Gebrauchstauglichkeit ist nur in den Eurocode-nahen
Normen vorgeschrieben, da eine sehr weitreichende Berücksichtigung
des plastischen Verformungsverhaltens bis hin zu vollplastischen
Berechnungsverfahren zugelassen ist. |
Für das nutzungsgerechte und dauerhafte Verhalten
eines Bauwerks sind übermäßige Schädigungen des
Betongefüges
sowie nichtelastische Verformungen des Betonstahls durch Einhaltung
von Spannungsgrenzen
zu vermeiden. |
|
|
| DIN 1045-1, 11.1 / DIN Fb 102, 4.4.1 / EC 2, 7.2 |
|
 |
|
Der Nachweis erfordert die Eingabe der beiden Grenzwerte
zul σc für den Beton und zul σs für
den Stahl. |
|
| Abb. Eigenschaftsblatt aus 4H-EC2QB |
|
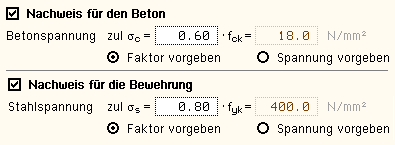 |
|
|
| Nach 7.2(2) sollen die Betondruckspannungen
zur Vermeidung von Längsrissen unter der charakteristischen (seltenen) Einwirkungskombination auf den empfohlenen Wert von
zul σc = 0.6 · fck begrenzt werden. |
Übersteigt die Betondruckspannung unter
quasi-ständiger Einwirkungskombinationden Wert 0.45 · fck, ist die
Tragfähigkeit
oder Dauerhaftigkeit des Bauwerks durch das Kriechen wesentlich beeinflusst. |
| Wird dieser Wert eingehalten, braucht nichtlinares
Kriechen nicht berücksichtigt zu werden. |
|
| Die Zugspannungen in der Betonstahlbewehrung
sind nach 7.2(5) bei direkten Einwirkungen (Lastbeanspruchung) unter der charakteristischen
(seltenen) Einwirkungskombination auf den Wert von zul σs = 0.8 · fyk zu begrenzen. |
|
| Bei reiner Zwangsbeanspruchung darf zul σs = fyk gelten. |
|
| Die Druck- und Zugspannungen werden auf Gebrauchslastniveau γc = γs = 1
mit den gewählten Spannungsdehnungslinien (s. Materialeigenschaften) ermittelt. |
|
| Der Spannungsnachweis wird folgendermaßen durchgeführt |
 |
| zunächst wird iterativ der vorhandene Bewehrungsquerschnitt
erhöht bis die zulässigen Stahlspannungen eingehalten sind |
|
 |
| anschließend erfolgt eine Überprüfung und ggf. Erhöhung
der Bewehrung auf der Druckseite bis auch der Betongrenzwert stimmt |
|
|
|
| Ist einer der beiden Grenzwerte = 0, wird der entsprechende Nachweis ignoriert. |
|
|
|
|
|
 |
|
| Besteht die Längsbewehrung
aus glasfaserverstärktem Kunststoff, führt das
Auftreten einer Stahldruckspannung zu einer Fehlermeldung. |
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| Tragende Bauteile, die einer hohen Anzahl von
Lastwechseln unterworfen sind (nicht ruhende Belastung), können
infolge Ermüdung versagen, auch wenn die Beanspruchung die für
die statischen Nachweise (ruhende Belastung) maßgebenden Materialfestigkeiten
nicht erreicht. |
| Für Tragwerke des üblichen Hochbaus
braucht i. A. kein Nachweis gegen Ermüdung geführt
zu werden. |
|
|
| DIN 1045-1, 10.8 / EC 2, 6.8 |
|
|
| Der Ermüdungsnachweis ist für
Beton und Bewehrung unter Biegung mit Längskraft
und Querkraft getrennt zu führen. |
|
| Abb. Eigenschaftsblatt aus 4H-EC2QB |
|
 |
|
|
| In pcae-Programmen werden - je nach Ausbaustufe
- folgende Nachweisverfahren angeboten |
 |
| Nachweis über schädigungsäquivalente
Schwingbreiten (Stufe 2, Grenzzustand der Tragfähigkeit) |
|
 |
| Vereinfachter Nachweis (Stufe 1, Grenzzustand
der Gebrauchstauglichkeit) |
|
|
|
| Bei beiden Verfahren erfolgt der Nachweis zunächst
für die Bewehrung (Eingabe der Spannungsschwingbreite zul Δσ).
Dazu wird der vorhandene Bewehrungsquerschnitt solange iterativ
erhöht bis für jede Bewehrungsgruppe die zulässige Schwingbreite
eingehalten ist. |
| Anschließend wird überprüft, ob der Beton unter
Druckbeanspruchung trägt (Eingabe des Zeitpunkts der Erstbelastung
des Betons t0). |
| Falls der Nachweis für Beton nicht erfüllt ist,
erfolgt keine weitere Bewehrungserhöhung, sondern es wird eine
Fehlermeldung ausgegeben. |
|
|
| Für den Nachweis sind mindestens zwei
Schnittgrößenkombinationen der ermüdungswirksamen
Einwirkungskombination vorzugeben. |
| Ist ein Wert (entweder Δσs oder t0) mit Null eingegeben, wird der Nachweis für
diese Materialgruppe nicht geführt. |
|
|
| Vereinfachter Nachweis (Stufe 1) |
|
| Der vereinfachte Nachweis ist mit der häufigen
zyklischen Einwirkungskombination zu führen. |
| Die Spannungen werden auf Gebrauchslastniveau γc = γs = 1 mit den gewählten
Spannungsdehnungslinien (s. Materialeigenschaften) ermittelt. |
|
| Bewehrung |
|
| gilt auch für die Querkraftbewehrung mit |
|
|
| Beton |
|
| Gilt auch für die Druckstreben von
querkraftbeanspruchten Bauteilen mit Querkraftbewehrung, wobei |
|
|
| Bauteile ohne rechnerisch erforderliche Querkraftbewehrung |
|
|
|
|
|
| Nachweis über schädigungsäquivalente Spannungsschwingbreiten (Stufe 2) |
|
Falls der vereinfachte Nachweis versagt,
kann anstelle eines expliziten Betriebsfestigkeitsnachweises
der
Nachweis gegen Ermüdung über schädigungsäquivalente
Spannungsschwingbreiten für die Bewehrung und schädigungsäquivalente
Druckspannungen für den Beton geführt werden. |
| Zur Berechnung ist eine Unterteilung in zyklische und nichtzyklische Einwirkungen vorzunehmen. |
| Die Grundkombination der nichtzyklischen
Einwirkungen entspricht der häufigen Einwirkungskombination,
die zyklische Einwirkung ist mit der ungünstigen nichtzyklischen
Grundkombination zu kombinieren. |
|
DIN 1045-1 und EC 2, NA-DE -
Im allgemeinen Hochbau sind die folgenden Einwirkungskombinationen
zu berücksichtigen |
 |
|
 |
| wahrscheinlicher Wert der Setzungen, sofern ungünstig wirkend |
|
 |
| häufiger Wert der Temperatureinwirkung, sofern ungünstig wirkend |
|
 |
| Einwirkungen aus Nutzlasten |
|
|
|
 |
Ständige Lasten, Setzungen, Temperatureinwirkungen
und quasiständige Nutzlasten sind nichtzyklische Einwirkungen und verändern daher nicht
die Spannungsschwingbreiten, sondern beeinflussen lediglich
das Nachweisniveau. |
|
|
|
|
|
Soll dagegen ein Industriebauwerk erstellt werden, ist die
ermüdungswirksame zyklische Einwirkung
(z.B. aus Kranbahn- oder Gabelstaplerbelastung) zusätzlich anzusetzen. |
Die Spannungen werden im Grenzzustand der Ermüdung mit den gewählten
Spannungsdehnungslinien
(s. Materialeigenschaften) ermittelt. |
|
| Bewehrung |
|
| Der Nachweis der Querkraftbewehrung wird mit dem vereinfachten Verfahren (s.o.) geführt. |
|
| Beton |
|
| Der Querkraftnachweis mit und ohne Querkraftbewehrung
wird mit dem vereinfachten Verfahren (s.o.) geführt. |
|
|
|
|
|
|
|
|
|
| Der Schwingnachweis ist nur für den Betonstahl zu führen. |
| Abb. Eigenschaftsblatt aus 4H-EC2QB |
|
 |
|
|
| Die Spannungsdifferenz aus Ober- und Unterlast |
|
| darf die eingegebene Schwingbreite zul Δσs nicht überschreiten. |
| Die Spannungen werden mit dem Parabel-Rechteck-Diagramm
für Beton und der bilinearen Spannungsdehnungslinie für die
Bewehrung ermittelt (s. Materialeigenschaften). |
|
Der Schwingbreitennachweis wird folgendermaßen durchgeführt:
der vorhandene Bewehrungsquerschnitt wird
iterativ erhöht bis
die zulässige Schwingbreite eingehalten ist.
Kann keine Lösung gefunden werden, wird eine Fehlermeldung ausgegeben. |
|
|
|
|
|
 |
|
| Besteht die Längsbewehrung
aus glasfaserverstärktem Kunststoff, wird der
Nachweis nicht geführt. |
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| Die Verformungen eines Bauteils oder eines Tragwerks
dürfen weder die ordnungsgemäße Funktion noch das Erscheinungsbild
des Bauteils selbst oder angrenzender Bauteile beeinträchtigen. |
| Es darf angenommen werden, dass das Erscheinungsbild
und die Gebrauchstauglichkeit eines Tragwerks nicht beeinträchtigt
werden, wenn der Durchhang unter der quasi-ständigen Einwirkungskombination
(bzw. unter Gebrauchslast) das 1/250-fache der Stützweite
(bei Kragträgern das 1/100 der Kraglänge) nicht überschreitet. |
|
| Der Grenzzustand der Verformung kann nachgewiesen
werden |
 |
| über die Begrenzung der Biegeschlankheit (ohne direkte Berechnung) |
|
 |
| nach Grasser/Thielen (Heft 240, DAfStb) |
|
|
|
|
| DIN 1045, 17.7.2 |
 |
| Begrenzung der Biegeschlankheit |
 |
| die Schlankheit von biegebeanspruchten
Bauteilen darf nicht größer sein als 35 |
|
 |
| bei Bauteilen, die Trennwände zu tragen haben,
soll die Schlankheit li/h ≤ 150/li (li und h in m) sein |
|
 |
| die Ersatzstützweite li wird nach Heft
240, DAfStb, angenommen zu li = α·L (α s. Heft 240, DAfStb) |
|
 |
| das Verfahren ist nur anwendbar, wenn α ≥ 0 gilt |
|
|
|
|
|
|
| DIN 1045-1, 11.3.2 |
 |
| Begrenzung der Biegeschlankheit |
 |
| die Schlankheit von biegebeanspruchten
Bauteilen darf nicht größer sein als 35 |
|
 |
| bei Bauteilen, die Trennwände zu tragen haben,
soll die Schlankheit li/d ≤ 150/li (li und h in m) sein |
|
 |
| die Ersatzstützweite li wird nach Heft
240, DAfStb, angenommen zu li = α·leff (α s. Tab.22 oder Heft 240, DAfStb) |
|
 |
| das Verfahren ist nur anwendbar, wenn α ≥ 0 gilt |
|
 |
| bei Leichtbeton sind die Grenzwerte mit ηE0.15 abzumindern |
|
|
|
|
|
|
| EC 2, 7.4.2 |
 |
|
|
|
| Heft 240, DAfStb |
 |
| Beschränkung der Durchbiegung
unter Gebrauchslast |
|
| Es wird die wahrscheinliche Durchbiegung
des Trägers zum Anfangs- sowie Endzeitpunkt der Lastaufbringung
ermittelt, die zwischen derjenigen im Zustand 1 (Träger
vollständig ungerissen) und Zustand 2 (Träger vollständig
gerissen) liegt. |
|
| Dazu wird die Ersatzstützweite li = α · L bestimmt über |
|
|
|
| Das Verfahren ist nur anwendbar, wenn gilt |
|
|
|
Die Berechnungen der Durchbiegungen setzen
sich zusammen aus dem Grundwert der Durchbiegung, Anteilen
aus der Bewehrungsmenge und -anordnung, Kriech- sowie
Schwindanteilen. |
| Aus den Durchbiegungen zu den
Zeitpunkten t0 und t∞ im reinen Zustand
1und 2 wird die wahrscheinliche Durchbiegung ermittelt zu |
|
|
|
|
|
| ComBAR GFK |
 |
| Besteht die Längsbewehrung
aus glasfaserverstärktem Kunststoff, wird der
Nachweis nicht geführt. |
|
|
|
|
|
|
 |
|
| Die Forderung nach einem angemessen dauerhaften
Tragwerk ist erfüllt, wenn dieses während seiner
Nutzungsdauer seine Funktion ohne wesentlichen Verlust
der Nutzungseigenschaften erfüllt. |
| Dabei sind die Umgebungsbedingungen zu
beachten, die die Mindestbetonfestigkeitsklasse und die
minimale Betondeckung der Bewehrung festlegen. |
| Das Bauteil ist in Expositionsklassen bestimmter
Kategorien einzuteilen, aus denen sich die Mindestwerte
ergeben. |
|
|
| DIN 1045-1, 6 / DIN-Fb 102, 2.4 |
 |
|
| Tab. 3: Expositionsklassen (DIN 1045-1 (8.08)) |
|
 |
|
|
|
|
| EC 2, 4 |
 |
|
| Tab. 4.1: Expositionsklassen |
|
|
|
Die Verschleißbeanspruchung des Betons darf
durch eine Vergrößerung der Betondeckung (Opferbeton)
berücksichtigt werden. |
 |
|
| mäßige Verschleißbeanspruchung (z.B. Industrieanlagen
mit Beanspruchung durch luftbereifte Fahrzeuge) |
|
|
|
 |
|
starke Verschleißbeanspruchung (z.B. Industrieanlagen
mit Beanspruchung durch luft- oder
vollgummibereifte Fahrzeuge) |
|
|
|
 |
|
sehr starke
Verschleißbeanspruchung (z.B. Industrieanlagen mit Beanspruchung durch
elastomer-
oder stahlrollenbereifte Fahrzeuge) |
|
|
|
|
|
| Mindestfestigkeitsklassen |
|
|
|
| Betondeckung |
|
| Mindestbetondeckung |
|
|
|
|
Bei Verschleißbeanspruchung: Vergrößerung der Betondeckung (s. NA, empf. XM1 5 mm, XM2 10 mm
und XM3 15 mm). |
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| DIN 1045, 15.3 / DIN 1045-1, 7.3.1 / DIN-Fb 102, 2.5.2.2.1 / EC 2, 5.3.2.1 |
 |
| Bei Plattenbalken- bzw. plattenbalkenähnlichen
Querschnitten darf vereinfachend die mitwirkende Plattenbreite
bei Durchführung der Nachweise unter Traglast- und Gebrauchslast
angesetzt werden. |
| Das Programm benötigt zur automatischen Ermittlung
Angaben über den Untersuchungsort (Endfeld, Innenfeld, Kragarm,
Stützbereich, Einfeldträger), die entsprechenden Feldlänge(n)
li sowie die vorhandenen Gurtbreiten bi. |
|
| Die mitwirkende Plattenbreite wird dann berechnet zu |
|
|
|
| EC 2: Für den Kragträger gilt l0 = 0.15 · l2 + l3; wird derzeit nicht unterstützt. |
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
|
|
| Die z.B. aus einer Finite-Element-Rechnung
stammenden Schnittgrößenkombinationen können i.A. nicht
direkt bemessen werden (wie bei Balken), da die Hauptachsen
der berechneten Schnittgrößen normalerweise nicht mit
der Richtung der zu bemessenden Bewehrung übereinstimmen. |
|
| Zur Umrechnung werden drei Verfahren angeboten,
wobei die Verfahren nach Baumann und EC 2 (6.92) nicht
für Faltwerke anwendbar sind |
|
|
| Die Verfahren basieren darauf, den Flächenträger
als Sandwich-platte mit einer Dicke von etwa 2·hs (bzw. 2·d) zu idealisieren. |
| Die an einem Flächenträgerelement
angreifenden Momente und Normalkräfte werden durch statisch
äquivalente Normalkräfte in den einzelnen Sandwichscheiben ersetzt
und diese für deren Wirkung bemessen. |
|
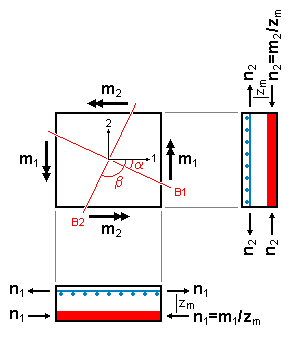 |
|
| Die Vorgehensweise der verschiedenen Verfahren
unterscheidet sich grundlegend darin, dass bei EC 2 (6.92) und
Thürlimann zunächst die auf das globale Koordinatensystem bezogenen
Schnittgrößen eines Punktes aus der FEM-Berechnung in Richtung
des Bewehrungskoordinatensystems zu transformieren sind. Mit
diesem transformierten Schnittsgrößenfeld wird die Bemessungsgröße
errechnet. |
| Die Baumann'schen Transformationsformeln ergeben
dagegen direkt die Bemessungsgrößen. |
| Nur das Verfahren von Thürlimann ist für
eine Bemessung von Biegung mit Normalkraft geeignet; EC 2 (6.92)
und Baumann können nur entweder Normalkräfte oder
Biegemomente transformieren. |
|
| Baumann |
|
| Die folgenden Formeln sind formuliert
für Schnittgrößen im Hauptachsensystem (1,2). Mit
x,y werden die Zug-Bewehrungslagen (in der Grafik
B1,B2) bezeichnet. Die z-Richtung entspricht der Richtung der Hauptdruckkraft. |
|
|
| Die in den o.a. Formeln verwendeten
Hauptschnittgrößen und Winkel müssen
noch weitere Bedingungen einhalten, die an dieser
Stelle nicht näher erläutert werden (s.
hierzu unter Literatur). |
|
|
|
|
| EC 2 (6.92) |
|
Die folgenden Formeln
sind formuliert für Schnittgrößen, die bereits auf
die Bewehrungsrichtungen x,y
(in der Grafik B1,B2)
bezogen sind. Sie gelten nur für orthogonal zueinander liegende Bewehrungsstäbe. |
|
 |
| für Platten mit my > mx |
|
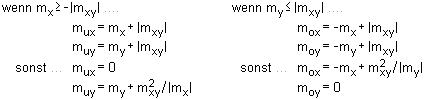 |
|
| Die Tragfähigkeit gilt als nachgewiesen, wenn gilt |
|
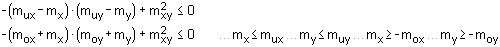 |
|
|
 |
| für Scheiben mit σy > σx |
|
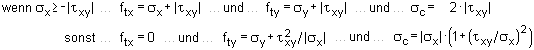 |
|
| Die Tragfähigkeit gilt als nachgewiesen, wenn gilt |
|
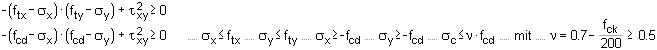 |
|
|
|
|
|
|
| Thürlimann |
|
Die folgenden Formeln sind formuliert
für Schnittgrößen, die bereits auf die Bewehrungsrichtungen
x,y
(in der Grafik B1, B2) bezogen sind. Sie gelten
nur für orthogonal zueinander liegende Bewehrungsstäbe. |
Um auch schiefwinklige Bewehrungsgitter
berücksichtigen zu können, werden die FEM-Schnittgrößen
zunächst
(wie auch bei orthogonalem Gitter) in die
jeweilige Bewehrungsrichtung transformiert und anschließend
nach den folgenden Formeln ausgewertet, in der Annahme,
dass sich eine obere Grenze der Beanspruchung ergibt |
|
| Für eine Schnittgrößenkombination ergeben sich bei der Bemessung von |
|
 |
|
| maximal zwei (je eine
Normalkraft max n für jede Bewehrungsrichtung B1, B2) |
|
 |
|
| maximal vier (je ein Biegemoment
für jede Bewehrungsrichtung und Lage B1o, B1u, B2o, B2u) |
|
 |
|
| maximal acht (je zwei, nämlich max
n, m und min n, m, für jede Bewehrungsrichtung und Lage B1o, B1u, B2o, B2u) |
|
|
|
| verschiedene Bemessungskombinationen. |
| Betondruckkraft |
|
| Die maßgebende Betondruckkraft ergibt sich zu |
|
|
|
|
|
| Transformation in die Bewehrungsrichtungen |
|
Die Transformation der kartesischen Schnittgrößen
nxx, nyy, nxy in
die Bewehrungsrichtungen αx,B1 und βx,B2
erfolgt über die Beziehungen |
|
|
|
|
|
| Hauptschnittgrößen |
|
| Die Hauptschnittgrößen
werden aus den kartesischen Schnittgrößen
nxx, nyy, nxy wie folgt ermittelt |
|
|
|
|
|
| Bewehrungsanordnung bei Platten und Faltwerken |
|
| Durch die Transformation der Berechnungsschnittgrößen
ergeben sich Bemessungsgrößen je Bewehrungsrichtung (B1, B2) und
-Lage (oben, unten), d.h. es werden 4 Schnitte B1o, B1u, B2o, B2u untersucht. |
| Aus der einachsigen Bemessung können dabei je Schnitt
2 Bewehrungen resultieren (Zug- und Druckbewehrung). |
| Bei geringer Belastung kann ein Gleichgewichtszustand gefunden
werden, bei dem nur Zugbewehrung erforderlich ist. Dann erhält jeder
Schnitt genau eine Bewehrung. |
| Ist jedoch eine hohe Belastung vorhanden, kann es notwendig
sein, Druckbewehrung einzulegen. |
| Sie wird mit der Zugbewehrung aus der Bemessung des anderen
Schnitts in der Bewehrungsrichtung maximiert. |
Ob und wie viel Druckbewehrung erforderlich ist, richtet sich
nach dem Grenzwert der bezogenen Druckzonenhöhe
lim xd / d.
Je geringer der Grenzwert ist, um so größer fällt die Druckbewehrung
aus. |
|
| Bei der Stabbemessung lässt sich mit lim xd / d
= -εc2u / (-εc2u + εs0) ein
optimaler Grenzwert bestimmen, bei dem die erforderliche
Bewehrung minimal wird. Für Normalbeton und B500 ergibt sich lim xd / d
= 0.62. |
|
| Bei der Flächenbemessung jedoch hängt es von der
Größe der Zugbewehrung im anderen Schnitt der betrachteten Bewehrungsrichtung
ab, welcher Grenzwert sinnvoll ist. |
| Da die Schnitte unabhängig voneinander bemessen werden,
ist es notwendig, den Grenzwert vorzugeben. |
| Bei zweiachsig belasteten Platten aus Normalbeton hat sich
ein Wert lim xd / d = 0.45 bewährt, jedoch ergibt bei einachsig gespannten
Platten der Wert aus der Stabbemessung eine wirtschaftlichere Bewehrung. |
|
|
|
|
|
|
|
|
|
| Die Bewehrungsrichtungen stimmen i. A. nicht
mit der Hauptquerkraftrichtung überein. Zudem ergeben
sich aus der Transformation der Biegeschnittgrößen auf
die Bewehrungsrichtungen keine zugehörigen Querkräfte. |
Das einachsige Tragverhalten ist aber Voraussetzung
zur Anwendung der Bemessungsverfahren nach den z.Z.
gültigen Normen. Um Flächenträger normenkonform bemessen zu können,
sind deshalb Transformationen in ein Balkenproblem notwendig. |
| Es kommen unterschiedliche Verfahren zur Anwendung. |
|
| DIN 1045 |
|
| Die Querkraftbemessung erfolgt nahezu unabhängig von der Biegebemessung auf
Basis von Schubspannungen. |
Als Bemessungsgröße wird die
Hauptquerkraft q1 gewählt. Schwierigkeiten
ergeben sich bei der Ermittlung des
inneren
Hebelarms, der Stahlrandabstände, des Querschnittzustands
(überdrückt, überzogen). |
| Der Einfachheit halber wird
die Hauptquerkraft in jeder Bewehrungsrichtung/-lage angesetzt. |
| Die Einzelergebnisse werden anschließend extremiert. |
|
| Bei Druckgliedern wird der Nachweis
der Hauptdruckspannungen für die minimale
Betondruckkraft (aus der Transformation) geführt. |
|
|
|
|
| DIN 1045-1 |
|
Die Querkraftbemessung erfolgt
auf Basis von Schubkräften, die stark richtungsabhängig
sind. Außerdem gehen in
die Bemessung die vorhandene Zugbewehrung und die Normalspannung ein – der Bezug zur
Biegebemessung ist
also sehr eng. |
| Deshalb wird die Querkraft vektoriell
in die beiden Bewehrungsrichtungen (s.a. 10.3.2 (2), DIN 1045-1 (8.08)) zerlegt. |
| Mit den zugehörigen Werten aus der Biegebemessung wird je Richtung
der maximale Bewehrungsanteil ermittelt. |
| Der erforderliche Bewehrungsquerschnitt ergibt sich aus der Summation der Einzelanteile. |
| Der wesentliche Vorteil des Verfahrens liegt darin, dass die Anteile in
den Bewehrungsrichtungen bekannt sind. |
| Dadurch ist es leicht möglich,
Aufbiegungen der Längsbewehrungen als mögliche
Querkraftbewehrung vorzusehen. |
| Nachteilig ist, dass das Bemessungsverfahren
wesentliche Größen – wie z.B. zur Bestimmung
von Längs- und Querabständen der Querkraftzulagen,
Weitergabe von Daten an Fertigteilwerke (VEd,
VRd,ct, VRd,max) – auch
(nur) richtungsbezogen liefert. Diese müssen
im Anschluss an die Bemessung zurücktransformiert werden. |
Daher wurde eine zweite Bemessungsvariante implementiert. Sie lehnt sich an die bekannte
Bemessung nach
DIN 1045 an und ermittelt die Schubbewehrung in Hauptquerkraftrichtung.
Sämtliche benötigten Größen werden zur Bemessung
in diese Richtung transformiert. |
|
|
|
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
| Die Bemessung von unbewehrtem Beton nach DIN Fb
102 wird nicht unterstützt. |
|
|
 |
|
|
|
| Nach 10.2(2) dürfen bei Bauteilen aus unbewehrtem
Beton höhere Betonfestigkeiten als C 35/45 bzw. LC 20/22
rechnerisch nicht ausgenutzt werden. |
|
| Biegebemessung |
|
| Nach 5.3.3(8) ist der Sicherheitsbeiwert
im Grenzzustand der Tragfähigkeit für die ständige
und vorübergehende Bemessungssituation mit
γc = 1.8 und für außergewöhnliche
Bemessungssituationen mit γc = 1.55 anzusetzen. |
Bildet sich eine klaffende Fuge aus,
die über den Schwerpunkt des Gesamtquerschnitts
geht, ist die
Tragfähigkeit überschritten. |
|
|
|
|
| Druckglieder aus unbewehrtem Beton (Th. II. Ord.) |
|
| Nach 8.6.7(3) darf der Bemessungswert der Normalkraft berechnet werden mit |
|
| Für unverschieblich ausgesteifte Bauteile gilt |
|
| Nach 8.6.7(2) hat die Schlankheit
unbewehrter Druckglieder i.d.R. den Wert λ = 0.85 nicht zu überschreiten. |
| Nach 8.6.7(1) ist für Druckglieder
aus unbewehrtem Beton mit lcol/h < 2.5
der Einfluss nach Th. II. O. vernachlässigbar. |
|
|
|
|
| Schubbemessung |
|
Nach 10.3.7(2) darf ein unbewehrtes
Bauteil als ungerissen angesehen werden, wenn die Hauptzugspannung
die Größe von 1.0 N/mm2 nicht überschreitet. |
Nach 10.3.7(3) ist ansonsten der Bemessungswert
der Querkrafttragfähigkeit am ungerissenen Restquerschnitt
zu berechnen. |
Dieser ergibt sich nach 10.3.3(2)
unter der Voraussetzung, dass die Betonzugspannungen stets kleiner
sind als fctk,0.05 / γc zu |
|
|
|
|
|
|
|
|
|
|
| Biegebemessung |
|
Nach 12.3.1(1) sind aufgrund der
geringeren Duktilität die Werte αcc,pl und αct,pl geringer anzusetzen
als die
Werte αcc und αct für bewehrten Beton. |
| Der axiale Widerstand ergibt sich nach 12.6.1(3) zu |
|
|
|
|
|
| Auswirkungen von Verformungen (Th. II. Ord.) auf Einzeldruckglieder und Wände |
|
| Nach 12.6.5.2(1) darf der Bemessungswert der Normalkraft berechnet werden mit |
|
| Für ausgesteifte Bauteile gilt |
|
| Nach 12.6.5.1(5) hat die Schlankheit
unbewehrter Druckglieder i.d.R. den Wert λ = 0.86 nicht zu überschreiten. |
|
|
|
|
| Schubbemessung |
|
Nach 12.6.3(3) darf ein unbewehrtes
Bauteil als ungerissen angesehen werden, wenn
die Hauptzugspannung
den Wert fctd nicht überschreitet. |
| Die Komponenten des Bemessungswerts
der Schubspannung sind nach 12.6.3(2) anzusetzen mit |
|
| Folgendes ist zu prüfen |
|
|
|
|
|
|
| |
|
|
|
| Bei Bauteilen aus unbewehrtem Beton dürfen
höhere Betonfestigkeiten als B 35 rechnerisch nicht ausgenutzt werden. |
| Der Last-Sicherheitsbeiwert ist mit 2.1 anzunehmen. |
Die Einflüsse von Schlankheit und ungewollter
Ausmitte dürfen näherungsweise durch Verringerung der zulässigen Last
mit dem Beiwert κ berücksichtigt werden |
|
Bildet sich eine klaffende Fuge aus, die über
den Schwerpunkt des Gesamtquerschnitts geht, ist die
Tragfähigkeit überschritten. |
|
|
|
|
|
 |
|
| In den Eurocode-nahen Normen werden keine Angaben
zur Ermittlung der durch eine wendelförmig angebrachte
Bewehrung zusätzlich aufnehmbaren Bruchnormalkraft gemacht. |
| Daher kann der günstige Einfluss einer Wendelbewehrung
nicht berücksichtigt werden. |
|
 |
|
| DIN 1045, 17.3.2 |
|
| Bei relativ großen Betonstauchungen führt eine
wendelartige Umschnürung des Druckgliedes zu einer Traglaststeigerung. |
Dieser Einfluss darf nur bei Druckgliedern mit
mindestens der Festigkeitsklasse B 25 und nur bis zu einer
Schlankheit ≤ 50 und einer Lastausmitte < 1/8 des Kern- bzw. Wendeldurchmessers in
Rechnung gestellt werden. |
| Außerdem ist der Einfluss der Zusatzmomente nach
Theorie II Ordnung zu berücksichtigen, d.h. die Eingabeschnittgrößen
sind nach Theorie II Ordnung zu ermitteln. |
|
|
|
|
|
 |
|
Die Eurocode-nahen Normen DIN 1045-1, DIN-Fb
102 und der Eurocode EC 2-1-1, EC 2-2 sind bis auf wenige
Unterschiede identisch. Im Folgenden wird sich auf die
aktuelle Norm EC 2-1-1 bezogen, Unterschiede zu den
anderen
Normen sind besonders gekennzeichnet. |
|
|
| Eine Zusammenstellung der korrespondierenden
Kapitel, Gleichungen und Tabellen ist hier zu finden. |
|
|
| Anmerkungen zur DIN 1045-1 |
|
| Die Ausgabe der Norm August 2008 kann in den pcae-Programmen
zur Bemessung herangezogen werden. |
| Unterschiede gegenüber
der Ausgabe Juli 2001 sind besonders gekennzeichnet. |
|
|
|
Die Eurocode-Normen sind nur
in Verbindung mit ihren nationalen Anhängen
gültig, die für
eine Auswahl an Parametern nationale Festlegungen treffen. |
| Im Folgenden wird sich auf
den Original-Code bezogen. |
| Unterschiede zum nationalen
Anhang von Deutschland (NA-DE) sind gekennzeichnet. |
|
|
|
|
 |
|
| DIN 1045-1, 8.6 / EC 2, 5.8.3 |
 |
| Bei Einzeldruckgliedern darf durch
Vergleich der Schlankheit mit Grenzwerten entschieden
werden, ob Einflüsse nach Theorie II. Ordnung
berücksichtigt werden müssen. |
| Einzeldruckglieder gelten als schlank,
wenn |
|
|
|
| DIN 1045-1 und EC 2, NA-DE |
|
|
|
Einzeldruckglieder in unverschieblich
ausgesteiften Tragwerken brauchen nicht nach Th.
II. Otd. untersucht
werden, wenn |
|
|
|
| EC 2 |
|
|
|
| Die Bemessung erfolgt mit dem Modellstützenverfahren. |
|
|
|
|
| DIN 1045-1, 8.6.5 / EC 2, 5.8.8 |
 |
| Das Modellstützenverfahren gilt für
Druckglieder mit einer Lastausmitte nach Theorie I. Ordnung
e ≥ 0.1·h, kann aber auch für Lastausmitten e
< 0.1·h angewendet werden. |
| Die Modellstütze ist eine am Fuß
eingespannte, symmetrisch bewehrte Kragstütze der
Länge l = l0/2, die eine einfach gekrümmte
Verformungsfigur aufweist. |
| Die Übertragung auf anders gelagerte
Stützen erfolgt über die Ersatzlänge l0. |
| Die Gesamtausmitte nach Theorie II. Ordnung
ergibt sich zu |
|
|
|
| Die Stütze wird bemessen für |
|
|
|
|
|
|
|
 |
|
| Die Eurocode-Normen gelten nur in Verbindung mit ihren nationalen Anhängen in dem jeweiligen Land, in dem das
Bauwerk erstellt werden soll. |
| Für ausgewählte Parameter können abweichend
von den Eurocode-Empfehlungen (im Eurocode-Dokument mit 'ANMERKUNG' gekennzeichnet) landeseigene Werte bzw. Vorgehensweisen angegeben
werden. |
In pcae-Programmen können die veränderbaren
Parameter in einem separaten Eigenschaftsblatt eingesehen
und ggf. modifiziert werden. |
 |
|
| Dieses Eigenschaftsblatt dient dazu, dem nach Eurocode zu
bemessenden Bauteil ein nationales Anwendungsdokument (NA) zuzuordnen. |
| NAe enthalten die Parameter der nationalen Anhänge der
verschiedenen Eurocodes (EC 0, EC 1, EC 2 ...) und ermöglichen den pcae-Programmen
das Führen normengerechter Nachweise, obwohl sie von Land zu Land
unterschiedlich gehandhabt werden. |
Die EC-Standardparameter (Empfehlungen ohne nationalen Bezug)
wie auch die Parameter des deutschen
nationalen Anhangs (NA-DE) sind grundsätzlich
Teil der pcae-Software. |
| Darüber hinaus stellt pcae ein Werkzeug zur
Verfügung, mit dem weitere NAe aus Kopien der bestehenden NAe erstellt
werden können. Dieses Werkzeug, das über ein eigenes Hilfedokument
verfügt, wird normalerweise aus der Schublade des DTE®-Schreibtisches
heraus aufgerufen. Einen direkten Zugang zu diesem Werkzeug liefert die
kleine Schaltfläche hinter dem Schraubenziehersymbol. |
|
|
|
 |
|
|
|
|
|
| unbewehrter Beton - Sicherheitsniveau |
|
|
|
|
|
|
| mitwirkende Plattenbreite |
|
|
|
|
|
|
vereinfachter Nachweis
der plastischen
Rotation |
|
|
|
|
|
|
| Mindeststützmoment am Auflagerrand |
|
|
|
|
|
|
| Druckglieder aus unbewehrtem Beton |
|
|
|
|
|
|
| Beton – Kriechen und Schwinden |
|
|
|
|
|
|
Beton (Spannungsdehnungslinie für
Verformungsberechnungen) |
|
|
|
|
|
|
Beton (Spannungsdehnungslinie für die
Bemessung, Parabel-Rechteck-Diagr.) |
|
|
|
|
Tabelle 3.1
Tabelle 11.3.1 |
|
|
|
|
|
| 4.2.2.3.2 a), Abb. 4.5 a) |
|
|
|
Betonstahl (Spannungsdehnungslinie für
Verformungsberechnungen) |
|
|
|
| 4.2.2.3.2 b), Abb. 4.5 b) |
|
|
|
Betonstahl (Spannungsdehnungslinie für
die Bemessung) |
|
|
|
|
|
|
Biegung mit oder ohne Längskraft und
Längskraft allein |
|
|
|
|
|
|
| Querkraft – auflagernahe Einzellasten |
|
|
|
|
|
|
Querkraft – Querkrafttragfähigkeit ohne
Bewehrung |
|
|
|
|
|
|
Querkraft – Querkrafttragfähigkeit für
ungerissenen Beton |
|
|
|
|
|
|
| Querkraft – innerer Hebelarm |
|
|
|
|
|
|
Querkraft – Grenzen für die
Druckstrebenneigung |
|
|
|
|
|
|
Querkraft – Querkrafttragfähigkeit mit
Bewehrung |
|
|
|
|
|
|
| Anschluss der Gurte an den Balkensteg |
|
|
|
|
|
|
| Schubkraftübertragung in Fugen |
|
|
|
|
|
|
| Schubbemessung für unbewehrten Beton |
|
|
|
|
|
|
Bemessung von Druckstreben –
Hauptdruckspannungsnachweis |
|
|
|
|
|
|
Nachweis gegen Ermüdung
– im
GZT (Stufe 2) |
|
|
|
|
|
|
Nachweis gegen Ermüdung
– im
GZG (Stufe 1) |
|
|
|
|
|
|
Nachweis gegen Ermüdung
– für Querkraft
im GZG (Stufe 1) |
|
|
|
|
|
|
| Begrenzung der Spannungen |
|
|
|
|
|
|
| Begrenzung der Betondruckspannungen |
|
|
|
|
|
|
| Begrenzung der Betonstahlspannungen |
|
|
|
|
|
|
| Begrenzung der Rissbreiten |
|
|
|
|
|
7.3.1 (105),
Tabelle 7.101N |
|
Anforderungen an die Begrenzung
der Rissbreite |
|
|
|
|
|
|
Grenzdurchmesser zur Begrenzung
der Rissbreite |
|
|
|
|
|
|
Mindestbewehrung zur Begrenzung
der Rissbreite |
|
|
|
|
|
|
Mindestbewehrung bei dickeren Bauteilen
unter zentrischem Zwang |
|
|
|
|
|
|
Begrenzung der Rissbreite ohne
direkte Berechnung |
|
|
|
|
|
|
| Berechnung der Rissbreite |
|
|
|
|
|
|
| Nachweis der Biegeschlankheit |
|
|
|
|
|
|
| allgemeine Bewehrungsregeln |
|
|
|
| 5.4.2.1.1 (101), 4.3.1.3 (109)P |
|
|
|
Mindestbewehrung für Biegeglieder
(duktiles Bauteilverhalten) |
|
|
|
|
|
|
| Mindeststützmomente am Endauflager |
|
|
|
|
|
|
Auslagerung der Längsbewehrung bei
Plattenbalken und Hohlkästen |
|
|
|
|
|
|
Mindestquerkraftbewehrung für
Biegeglieder |
|
|
|
|
|
|
Mindestquerkraftbewehrung für Platten bei
vEd ≤ vRd,ct |
|
|
|
|
|
|
| Mindestquerkraftbewehrung für Platten |
|
|
|
|
|
|
| Querbewehrung von Platten |
|
|
|
|
|
|
Mindestbewehrung für stabförmige
Druckglieder (Stützen) |
|
|
|
|
|
|
Querbewehrung für stabförmige
Druckglieder (Stützen) |
|
|
|
|
|
|
Mindestbewehrung für flächenhafte
Druckglieder (Wände) |
|
|
|
|
|
|
Mindestbügelbewehrung für flächenhafte
Druckglieder (Wände) |
|
|
|
|
|
|
 |
|
|
 |
DIN 1055-100 Einwirkungen auf Tragwerke
– Teil 100: Grundlagen der Tragwerksplanung,
Sicherheitskonzept und Bemessungsregeln, Deutsches
Institut für Normung e.V., Ausgabe März
2001 |
|
 |
| DIN 1045 Beton und Stahlbeton: Bemessung
und Ausführung, Deutsches Institut für
Normung e.V., Ausg. Juli 1988 |
|
 |
DIN 1045-1 Tragwerke aus Beton, Stahlbeton
und Spannbeton, Teil 1: Bemessung und Konstruktion,
Deutsches Institut für Normung e.V., Ausgaben
Juli 2001 und August 2008 |
|
 |
| Erläuterungen zu DIN 1045-1,
Heft 525, Deutscher Ausschuss für Stahlbeton,
Beuth Verlag GmbH, 2003 |
|
 |
| Berichtigung 1 zum DAfStb-Heft 525,
Mai 2005 |
|
 |
| DIN-Fachbericht 102: Betonbrücken,
Deutsches Institut für Normung e.V., Ausgabe
März 2009 |
|
 |
| DIN 4102-4: Brandverhalten von Baustoffen
und Bauteilen – Teil 4: Zusammenstellung und Anwendung
klassifizierter Baustoffe, Bauteile und Sonderbauteile,
Ausgabe März 1994 |
|
 |
| DIN 4102-4/A1: Brandverhalten von
Baustoffen und Bauteilen – Teil 4: Zusammenstellung
und Anwendung klassifizierter Baustoffe, Bauteile
und Sonderbauteile, Änderung A1, Ausgabe November
2004 |
|
 |
| DIN 4102-22: Brandverhalten von Baustoffen
und Bauteilen – Teil 22: Anwendungsnorm zu 4102-4
auf der Bemessungsbasis von Teilsicherheitsbeiwerten,
Ausgabe November 2004 |
|
 |
| DIN EN 1990, Eurocode: Grundlagen
der Tragwerksplanung; Deutsche Fassung EN 1990:2002
+ A1:2005 + A1:2005/AC:2010, Deutsches Institut
für Normung e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1990/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode: Grundlagen
der Tragwerksplanung; Deutsches Institut für
Normung e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-1, Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-1: Allgemeine Einwirkungen
auf Tragwerke – Wichten, Eigengewicht und Nutzlasten
im Hochbau; Deutsche Fassung EN 1991-1-1:2002 +
AC:2009, Deutsches Institut für Normung e.V.,
Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-1/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-1: Allgemeine Einwirkungen
auf Tragwerke – Wichten, Eigengewicht und Nutzlasten
im Hochbau; Deutsches Institut für Normung
e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-2, Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-2: Brandeinwirkungen auf
Tragwerke; Deutsche Fassung EN 1991-1-2:2002 + AC:2009,
Deutsches Institut für Normung e.V., Ausgabe
Dezember 2010 |
|
 |
| DIN EN 1991-1-2/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-2: Brandeinwirkungen auf
Tragwerke; Deutsches Institut für Normung e.V.,
Ausg. Dezember 2010 |
|
 |
| DIN EN 1991-1-3, Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-3: Allgemeine Einwirkungen
– Schneelasten; Deutsche Fassung EN 1991-1-3:2003
+ AC:2009, Deutsches Institut für Normung e.V.,
Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-3/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-3: Allgemeine Einwirkungen
– Schneelasten; Deutsches Institut für Normung
e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-4, Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-4: Allgemeine Einwirkungen
– Windlasten; Deutsche Fassung EN 1991-1-4:2005
+ A1:2010 + AC:2010, Deutsches Institut für
Normung e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-4/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-4: Allgemeine Einwirkungen
– Windlasten; Deutsches Institut für Normung
e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-5, Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-5: Allgemeine Einwirkungen
– Temperatureinwirkungen; Deutsche Fassung EN 1991-1-5:2003
+ AC:2009, Deutsches Institut für Normung e.V.,
Ausgabe Dezember 2010 |
|
 |
| DIN EN 1991-1-5/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 1: Einwirkungen
auf Tragwerke – Teil 1-5: Allgemeine Einwirkungen
– Temperatureinwirkungen; Deutsches Institut für
Normung e.V., Ausgabe Dezember 2010 |
|
 |
| DIN EN 1992-1-1, Eurocode 2: Bemessung
und Konstruktion von Stahlbeton- und Spannbetonbauteilen
– Teil 1-1: Allgemeine Bemessungsregeln und Regeln
für den Hochbau; Deutsche Fassung EN 1992-1-1:2004
+ AC:2010, Deutsches Institut für Normung e.V.,
Ausgabe Januar 2011 |
|
 |
| DIN EN 1992-1-1/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 2: Bemessung
und Konstruktion von Stahlbeton- und Spannbetontragwerken
– Teil 1-1: Allgemeine Bemessungsregeln und Regeln
für den Hochbau; Deutsches Institut für
Normung e.V., Ausgabe April 2013 |
|
 |
DIN EN 1992-1-2, Eurocode 2: Bemessung
und Konstruktion von Stahlbeton- und Spannbetontragwerken
– Teil 1-2: Allgemeine Regeln – Tragwerksbemessung
für den Brandfall; Deutsche Fassung EN 1992-1-2:2004
+ AC:2008,
Deutsches Institut für Normung e.V., Ausgabe
Dezember 2010 |
|
 |
| DIN EN 1992-1-2/NA, Nationaler Anhang
– National festgelegte Parameter – Eurocode 2: Bemessung
und Konstruktion von Stahlbeton- und Spannbetontragwerken
– Teil 1-2: Allgemeine Regeln – Tragwerksbemessung
für den Brandfall; Deutsches Institut für
Normung e.V., Ausgabe Dezember 2010 |
|
 |
DIN V ENV 1992-1-2, Eurocode 2 (Vornorm):
Planung von Stahlbeton- und Spannbetontragwerken
– Teil 1-2: Allgemeine Regeln – Tragwerksbemessung
für den Brandfall; Deutsche Fassung ENV 1992-1-2:1995,
Ausgabe Mai 1997 |
|
 |
| Nationales Anwendungsdokument (NAD)
Richtlinie zur Anwendung von DIN V ENV 1992-1-2: 1997-05
Eurocode 2: Planung von Stahlbeton- und Spannbetontragwerken
– Teil 1-2: Allgemeine Regeln – Tragwerksbemessung
für den Brandfall. DIN-Fachbericht 92, 2000 |
|
 |
Normenausschuss Bauwesen (NABau) –
Stand der Auslegungen, Deutsches Institut für Normung
e.V.,
www.nabau.din.de |
|
|
|
|
|
|
|
|
|
| Schnittgrößentransformation bei Flächenträgern |
|
|
 |
T. Baumann: Zur Frage der Netzbewehrung
von Flächenträgern. Der Bauingenieur 47
(1972), Heft 10,
Springer Verlag, 1972 |
|
 |
DIN V ENV 1992-1-1, Eurocode 2 (Vornorm):
Planung von Stahlbeton- und Spannbetontragwerken
– Teil 1-1:
Grundlagen und Anwendungsregeln für den Hochbau,
Deutsches Institut für Normung e.V., Ausgabe Juni
1992 |
|
 |
| B. Thürlimann: Anwendungen der
Plastizitätstheorie auf Stahlbeton. Vorlesung
zum Fortbildungskurs für Bauingenieure von
13.-15. April 1983. Institut für Baustatik
und Konstruktion, Eidgenössische Technische
Hochschule Zürich |
|
 |
K. Holschemacher: Stahlbetonplatten
– Neue Aspekte zur Bemessung, Konstruktion und Bauausführung,
Bauwerk-Verlag GmbH, 2005 |
|
|
|
|
|
|
 |
D. Bertram & N. Bunke: Erläuterungen
zu DIN 1045 Beton und Stahlbeton, Ausgabe 07.88,
Heft 400,
Deutscher Ausschuss für Stahlbeton, Beuth Verlag
GmbH, 1989 |
|
 |
K. Zilch, G. Zehetmaier: Bemessung
im konstruktiven Betonbau – Nach DIN 1045-1
und DIN EN 1992-1-1,
Springer Verlag, 2006 |
|
 |
| R. Avak: Stahlbetonbau in Beispielen,
Teil 1, 4. neu bearbeitete und erweiterte Auflage,
Werner Verlag, 2004 |
|
 |
A. Goris: Stahlbetonbau-Praxis nach
DIN 1045 neu, 2. aktualisierte und erweiterte Auflage,
Bauwerk Verlag GmbH, 2004 |
|
 |
| F. Fingerloos: DIN 1045 Ausgabe 2008
Tragwerke aus Beton und Stahlbeton, Teil 1: Bemessung
und Konstruktion, Kommentierte Kurzfassung, 3. Auflage,
Fraunhofer IRB und Beuth Verlag, 2008 |
|
 |
| Erläuterungen zu DIN EN 1992-1-1
und DIN EN 1992-1-1/NA (Eurocode 2), Heft 600, Deutscher
Ausschuss für Stahlbeton, 1. Auflage, 2012 |
|
 |
| F. Fingerloos, J. Hegger, K. Zilch:
Eurocode 2 für Deutschland, Kommentierte Fassung,
Beuth Verlag und Verlag Wilhelm Ernst & Sohn,
2012 |
|
 |
O. Wommelsdorff, A. Albert: Stahlbetonbau - Bemessung
und Konstruktion, Teil 1, 10. Auflage,
Werner Verlag, 2011 |
|
 |
O. Wommelsdorff, A. Albert: Stahlbetonbau - Bemessung
und Konstruktion, Teil 2, 9. Auflage,
Werner Verlag, 2012 |
|
|
|
|
|
|
 |
D. Bertram & N. Bunke: Erläuterungen
zu DIN 1045 Beton und Stahlbeton, Ausgabe 07.88,
Heft 400,
Deutscher Ausschuss für Stahlbeton, Beuth Verlag
GmbH, 1989 |
|
 |
E. Grasser: Bemessung für Biegung
mit Längskraft, Schub und Torsion, Betonkalender
Teil I,
Verlag Ernst und Sohn, 1985 |
|
 |
Deutscher Beton- und Bautechnik-Verein
e.V.: Beispiele zur Bemessung nach DIN 1045-1,
Band 1: Hochbau, 2. Auflage, Ernst und Sohn Verlag,
2005 |
|
 |
D. Bertram: Erläuterungen zu DIN 4227
Spannbeton (Teil I, Abschnitt 12), Heft 320,
Deutscher Ausschuss für Stahlbeton, Beuth Verlag
GmbH, 1989 |
|
 |
| H. Friemann: Schub und Torsion in
geraden Stäben, Werner-Verlag GmbH, Düsseldorf,
1983 |
|
 |
| K. Zilch und A. Rogge: Bemessung von
Stahlbeton- und Spannbetonbauteilen im Brücken-
und Hochbau, Betonkalender 2004 |
|
 |
| G. Valentin und G. Kidery: Stahlbetonbau,
Manz Verlag Schulbuch, Wien 2001 |
|
 |
| P. Mark: Ein Bemessungsansatz für
zweiachsig durch Querkräfte beanspruchte Stahlbetonbalken
mit Rechteckquerschnitt, Heft 5, Beton- und Stahlbetonbau
100 (2005) |
|
|
|
|
|
| mitwirkende Plattenbreite |
|
|
 |
| E. Grasser, G. Thielen: Hilfsmittel
zur Berechnung der Schnittgrößen und Formänderungen
von Stahlbetontragwerken. Heft 240, DAfStb, Beuth
Verlag Berlin, 1991 |
|
|
|
|
|
|
 |
F. Leonhardt & E. Mönnig: Vorlesungen über Massivbau,
Zweiter Teil: Sonderfälle der Bemessung im Stahlbetonbau, Dritte Auflage, Springer-Verlag, 1986 |
|
 |
F. Leonhardt & E. Mönnig: Vorlesungen über Massivbau,
Dritter Teil: Grundlagen zum Bewehren
im Stahlbetonbau, Springer-Verlag, 1977 |
|
 |
R. Eligehausen & R. Gerster: Das
Bewehren von Stahlbetonbauteilen,
Heft 399, Deutscher
Ausschuss für Stahlbeton, Beuth Verlag GmbH, 1993 |
|
 |
U. Hottmann & K. Schäfer: Bemessen von Stahlbetonbalken
und -wandscheiben mit Öffnungen,
Heft 459, Deutscher Ausschuss für Stahlbeton, Beuth
Verlag GmbH, 1996 |
|
 |
J. Hegger et al.: Bewehren nach Eurocode 2,
Heft 599, Deutscher Ausschuss für Stahlbeton, Beuth
Verlag GmbH, 2013 |
|
 |
Teil 1: Erläuterungen zu DIN EN 1991-1-1 und DIN EN 1992-1-1/NA,
Heft 600, Deutscher Ausschuss für Stahlbeton, 2. überarbeitete Auflage, Beuth Verlag GmbH, 2020 |
|
 |
M. Schellenbach-Held & S. Ehmann: Stahlbetonträger mit
großen Öffnungen,
Heft 3, Beton- und Stahlbetonbau 97, Verlag Ernst & Sohn, 2002 |
|
 |
D. Bertram & N. Bunke: Erläuterungen
zu DIN 1045 Beton und Stahlbeton, Ausgabe 07.88,
Heft 400, Deutscher Ausschuss für Stahlbeton, Beuth
Verlag GmbH, 1989 |
|
 |
E. Grasser: Bemessung für Biegung mit
Längskraft, Schub und Torsion,
Betonkalender Teil I, Verlag Ernst und Sohn, 1985 |
|
 |
D. Bertram: Erläuterungen zu DIN 4227
Spannbeton (Teil I, Abschnitt 12),
Heft 320, Deutscher Ausschuss für Stahlbeton, Beuth
Verlag GmbH, 1989 |
|
 |
E. Grasser & G. Thielen: Hilfsmittel
zur Berechnung der Schnittgrößen und Formänderungen
von
Stahlbetontragwerken, Heft 240, Deutscher Ausschuss
für Stahlbeton, Beuth Verlag GmbH, 1991 |
|
 |
F. Fingerloos, G. Stenzel: Konstruktion und Bemessung von Details,
Betonkalender Teil 2, Verlag Ernst und Sohn, 2007 |
|
 |
H. Bachmann, M. Tillmann, S. Urban: Bauen mit Betonfertigteilen,
Betonkalender Teil 1, Verlag Ernst und Sohn, 2021 |
|
|
|
|
|
|
| Verfahren nach Norm |
 |
 |
| G. König & N. Viet Tue: Grundlagen
und Bemessungshilfen für die Rissbreitenbeschränkung
im Stahlbeton und Spannbeton, Heft 466, Deutscher
Ausschuss für Stahlbeton,
Beuth Verlag GmbH, 1996 |
|
 |
| G. Lohmeyer, K. Ebeling: Weiße Wannen
einfach und sicher, Verlag Bau+Technik, 11. Auflage, 2018 |
|
 |
| H. K. Hilsdorf: Zeitabhängige Betonverformungen (EC 2 - Abschnitte 2.5.5, 3.1.2.5 und Anhang 1), Heft 425, Deutscher
Ausschuss für Stahlbeton, 1992 |
|
|
| Verfahren nach Schießl |
 |
 |
P. Schießl: Grundlagen der Neuregelung
zur Beschränkung der Rissbreite, Heft 400,
Deutscher Ausschuss für Stahlbeton, Beuth Verlag
GmbH, 1989 |
|
 |
| J. Bergfelder, J. Dittfach: Beschränkung
der Rissbreite bei Ortbetonpfählen, Beton-
und Stahlbetonbau 87, 1992 |
|
|
| Verfahren nach Noakowski |
 |
 |
P. Noakowski: Verbundorientierte,
kontinuierliche Theorie zur Ermittlung der Rissbreite,
Beton- und Stahlbetonbau 80, 1985 |
|
 |
| K. Frank, M. Litzenburger, G. Peters:
Rissnachweis nach Noakowski, aufbereitet für den
Taschenrechner, Heft 5, Bautechnik 65, 1988 |
|
|
|
|
|
| Schwingbreiten- / Ermüdungsnachweis |
|
|
 |
| K. Zilch und A. Rogge: Bemessung von
Stahlbeton und Spannbetonbauteilen im Brücken- und
Hochbau, Betonkalender 2004, Verlag Ernst &
Sohn, 2004 |
|
 |
K. Zilch, G. Zehetmaier und C. Gläser:
Ermüdungsnachweis bei Massivbrücken, Betonkalender
2004,
Verlag Ernst & Sohn, 2004 |
|
 |
J. Hegger, W. Roeser, R. Beutel, N.
Kerkeni: Konstruktion und Bemessung von Industrie-
und Gewerbebauten
nach DIN 1045-1, Betonkalender 2006, Verlag Ernst
& Sohn, 2006 |
|
 |
M. Heunisch, C.-A. Graubner, C. Hock:
Berechnung und Bemessung von Kranbahnen, Betonkalender
2006,
Verlag Ernst & Sohn, 2006 |
|
|
|
|
|
| vereinfachter Brandschutznachweis für Druckglieder |
|
|
 |
H. M. Bock, E. Klement: Brandschutz-Praxis
für Architekten und Ingenieure, 2. Auflage,
Bauwerk-Verlag GmbH, 2006 |
|
 |
N. A. Fouad, A. Schwedler: Brandschutz-Bemessung
auf einen Blick nach DIN 4102,
Bauwerk-Verlag GmbH, 2006 |
|
 |
Musterliste der Technischen Baubestimmungen,
Kap.3 Techn. Regeln zum Brandschutz,
Betonkalender
2007, Teil 2 |
|
 |
F. Fingerloos, E. Richter: Zur Heißbemessung
von Stahlbetonstützen,
Der Prüfingenieur, April 2007 |
|
|
|
|
|
| Brandbemessung n. DIN EN 1992-1-2 (EC 2 für Brandbeanspruchung) |
|
|
 |
Normenhandbuch Eurocodes – Spezialband
Tragwerksbemessung für den Brandfall.
Vom DIN konsolidierte Fassung, Beuth Verlag, 2012 |
|
 |
M. Cyllok & M. Achenbach: Anwendung
der Zonenmethode für brandbeanspruchte Stahlbetonstützen,
Beton- und Stahlbetonbau 104, Heft 12, 2009 |
|
 |
| M. Cyllok & M. Achenbach: Bemessung
von Stahlbetonstützen im Brandfall: Absicherung
der nicht-linearen Zonenmethode durch Laborversuche,
Beton- und Stahlbetonbau 106, Heft 1, 2011 |
|
 |
| K. Zilch, A. Müller, C. Reitmayer:
Erweiterte Zonenmethode zur brandschutztechnischen
Bemessung von Stahlbetonstützen, Bauingenieur
Band 85, 2010 |
|
 |
| R. Hinkelmann: Efficient Numerical
Methods and Information-Processing Techniques for
Modelling Hydro- and Environmental Systems. Springer-Verlag,
2005 |
|
 |
J. Hildebrand: Berechnung nichtlinearer
Diffusionsvorgänge in Strukturen mit der Randelementmethode.
VDI Verlag GmbH, 1998 |
|
 |
H. Köhne: Digitale und analoge
Lösungsmethoden der Wärmeleitungsgleichung.
Westdeutscher Verlag, 1970 |
|
 |
H. Pennekamp: Ein analytisches Näherungsverfahren
zur Berechnung mehrdimensionaler, instationärer
Temperaturfelder in geometrisch einfachen Strukturen.
Dissertation, Fakultät für Bergbau und
Hüttenwesen der TU Aachen, 1973 |
|
|
|
|
|
| Druckzonendicke / Nachweis der Dichtigkeit |
|
|
 |
DAfStb-Richtlinie: Wasserundurchlässige
Bauwerke, Deutscher Ausschuss für Stahlbeton,
Ausg. Dezember 2017 |
|
 |
DAfStb-Richtlinie: Betonbau beim Umgang
mit wassergefährdenden Stoffen,
Deutscher Ausschuss für Stahlbeton, Ausgabe
März 2011 |
|
 |
Erläuterungen zur DAfStb-Richtlinie
wasserundurchlässige Bauwerke,
Heft 555, Deutscher Ausschuss für Stahlbeton,
2006 |
|
|
|
|
|
| Bemessung einer Rahmenecke |
|
|
 |
O. Wommelsdorff, A. Albert: Stahlbetonbau – Bemessung
und Konstruktion, Teil 2, 9. Auflage,
Werner Verlag, 2012 |
|
 |
| K. Beer: Bewehren nach DIN EN 1992-1-1 (EC2),
3. Auflage, Springer Vieweg, 2012. |
|
 |
| Bewehren nach Eurocode 2:
Heft 599, Deutscher Ausschuss für Stahlbeton, 2013 |
|
|
|
|
|
|
 |
| Merkblätter des Deutschen Beton-
und Bautechnik-Vereins e.V.: Beton und Betonstahl,
Fassung Januar 2008 |
|
 |
| U. Quast: Nichtlineare Statik im Stahlbetonbau.
Bauwerk Verlag, 2007 |
|
 |
G. Allgöwer: Bemessung von Stahlbetondruckgliedern
unter zweiachsiger Biegung mit Interaktionsdiagrammen
nach Theorie II Ordnung. Dissertation, Fakultät
für Bauingenieurwesen, Architektur und Stadtplanung
der
TU Cottbus, 2001 |
|
 |
| S. Köseoglu: Treppen. Betonkalender
Teil II, Verlag Ernst und Sohn, 1980 |
|
 |
| Schöck ComBAR GFK, Zulassung Z-1.6-238
vom 8.7.2019, Deutsches Institut für Bautechnik |
|
|
|
|
|
|
|
 |
 |
 |